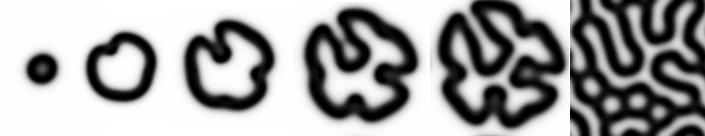
Published September 2025 as part of the proceedings of the first Alpaca conference on Algorithmic Patterns in the Creative Arts, according to the Creative Commons Attribution license. Copyright remains with the authors.
doi:10.5281/zenodo.17084384
This paper explores how Reaction-Diffusion (RD) systems can generate motifs resembling folk designs, suggesting that cultural aesthetics may emerge from nature-inspired algorithms and shared human perception. By examining RD patterns, it proposes that the similarity between these algorithmically generated patterns and traditional motifs may reflect universal principles governing both natural and human-made systems.
Note: This paper includes several interactive code demos (marked throughout) that allow readers to experiment directly with the Reaction-Diffusion systems discussed.
Why do folk motifs across distant cultures often resemble forms in nature?
Folk designs have long been a central element of human culture, symbolizing shared values, traditions, and natural phenomena. This ‘cultural memory’ is not merely a collection of historical facts, but a dynamic, evolving repository of shared experiences, values, and artistic expressions passed down through generations, often embedded within symbolic forms like folk motifs. In this paper, we explore the connection between nature, mathematics, and recurring forms found in traditional motifs.
At the core of this inquiry are Reaction-Diffusion (RD) systems—mathematical models describing how two or more chemicals interact to produce complex patterns. Inspired by natural processes, these systems have been studied extensively in scientific fields like chemistry and biology. However, their potential to generate culturally significant and aesthetically pleasing motifs remains largely underexplored. These motifs, born in code, don’t just echo tradition—they may uncover its algorithmic root. The pattern doesn’t need to be passed down—it emerges.
By comparing algorithmic outputs with folk designs, we aim to explore the possibility that human aesthetics might emerge from universal natural processes. This investigation asks: What can Reaction-Diffusion systems reveal about the emergence of pattern in human culture?
RD systems (Turing, 1952 1), while rooted in simple mathematical principles, are capable of producing unexpectedly intricate patterns. These patterns emerge from the interaction of two or more chemicals, often referred to as chemical A and B in a spatial grid, which diffuse across space and react with one another. The results, though governed by basic rules, have an organic and almost lifelike quality, mimicking the complexity found in nature.
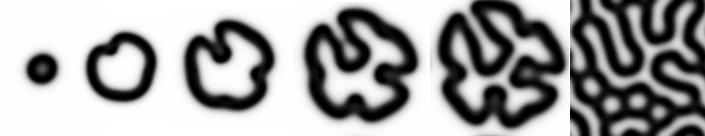
At their core, RD systems describe a kind of chemical tug-of-war: one chemical activates while the other suppresses. This “feed vs kill” dynamic, as seen in the Gray-Scott model (a canonical reaction–diffusion system), leads to emergent complexity—blobs, spots, stripes—that wouldn’t appear if each chemical diffused independently.3 4
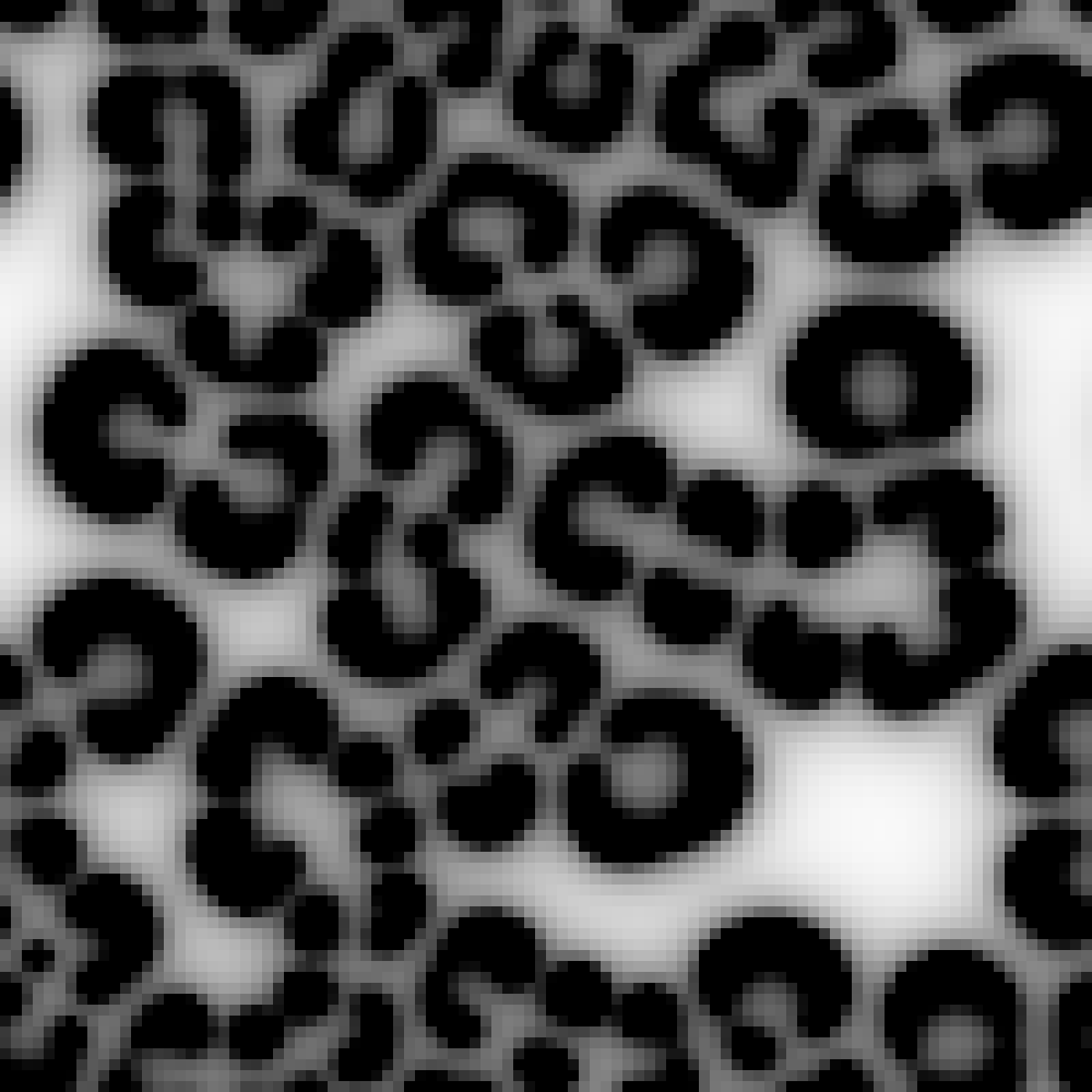
Surprisingly, RD systems can generate patterns strikingly similar to those found in nature—think of the stripes of a zebra, the spots of a leopard, the spirals of a snail shell, or even the ripples of sand dunes. This connection between RD patterns and natural forms is not merely coincidental, but highlights how simple algorithms can produce highly recognizable motifs.


Figure 2: A comparison of RD-generated patterns with natural examples—zebra.

The patterns generated by Reaction-Diffusion systems, while born from scientific principles, exhibit remarkable aesthetic qualities that resonate with human visual perception.
At first glance, these algorithmically generated designs may seem purely mathematical or abstract, but a closer examination reveals their striking resemblance to motifs traditionally found in folk art across diverse cultures. These visual rhymes aren’t accidental.
Interactive demo 1.1 uses the same code as Demo 1, with a central square seed for chemical B instead of a randomized start (see Annex 1).

The convergence of science and art suggests that the principles behind RD systems could be a key to understanding the origins of these motifs—shapes, symbols, and forms that have persisted for generations.
Reaction-Diffusion systems and folk art both rely on local interactions generating global order
Folk art often reflects the natural world, drawing on organic patterns found in plants, animals, and landscapes. From intricate floral designs in textiles to geometric shapes in pottery, many motifs are not only aesthetically pleasing but also convey cultural meaning and shared values.
Yet, as we explore RD patterns, it becomes increasingly apparent that the underlying algorithms produce forms remarkably similar to these traditional designs, hinting at a deeper connection between nature, mathematics, and human culture.
Figure 5 Traditional Motif (left) vs RD-generated design (unconstrained)


Figure 6 Traditional Motif (left) vs RD-generated design (with applied constraints)
Take, for instance, the pixel-like symmetry and nested geometric shapes of Romanian embroidery patterns, often seen on traditional textiles. The motif on the left, with its grid-based repetition and bold red-white contrast, shares an uncanny visual logic with the RD-generated design on the right. Though born from different systems—one cultural, one algorithmic—both arrive at structured, mirrored compositions built from small units interacting in space.
These motifs, in part, emerge due to specific tweaks and adjustments made to the parameters of the model, further refining the resemblance to folk art patterns.
What is truly compelling is that this similarity is not coincidental. RD systems—driven by the diffusion of chemicals and their reactive interplay—generate patterns that are inherently dynamic, replicating flow and organic variation that characterize natural forms. As chemicals diffuse and react across a space, they form dynamic structures—often including spirals, loops, and bands—that closely resemble motifs seen in folk art.


Figure 7 Traditional Motif (left) vs RD-generated design (RD evolved through constraint)
This demonstration showcases a significantly adapted Reaction-Diffusion-like system designed to generate complex folk-inspired patterns.
The generative power of RD models aligns with the fundamental principles of folk art creation: simplicity, repetition, and an inherent connection to natural patterns. Just as folk artists may unconsciously echo the shapes they observe in nature, RD systems appear to ‘mirror’ these forms through algorithmic processes. This synthesis between science and culture leads to the intriguing possibility that cultural aesthetics could, in part, be grounded in the natural principles of pattern formation that RD systems exemplify.
By studying RD-generated motifs, we can begin to appreciate how nature’s processes might have guided the development of folk motifs. The contrast between the simplicity of the underlying rules of Reaction-Diffusion and the complexity of the resulting patterns invites us to reconsider the ways in which we generate and interpret cultural designs. The very act of observing these patterns—whether in nature, on a canvas, or in a digital model—may reveal something fundamental about our collective human perception of beauty.
Additional Controls (repeat, alternate +/-, or simply let it evolve by itself): a (diffusion rate dA+), q (dA-) b (diffusion rate dB+), g (dB-) k (kill rate+), i (kill rate-) f (feed rate+), r (feed rate-);
This interactive model represents a sophisticated and extensively customized system, building upon Reaction-Diffusion principles to generate highly elaborate motifs.
In the end, these connections between RD systems and folk patterns raise fascinating questions about the universality of design in human culture. Could these mathematical processes be more than just a scientific curiosity? Could they actually explain how some of humanity’s most enduring artistic traditions came to be?
Some of the visual motifs emerging from RD-generated forms—such as spirals, waves, loops, or rhombi—demonstrate a striking resemblance to patterns found across diverse periods and cultural traditions, from Romanian embroidery to Mexican mosaics or Greek pottery.
This widespread recurrence of visually similar forms in folk patterns, characterized by repetition and self-similarity (Lidwell et al., 2010 8), raises questions about whether they result from cultural transmission—shared visual conventions learned over time—or from universal perceptual biases. Gombrich (1960 9) emphasizes that perception is not passive but shaped by prior experience, as viewers actively interpret images using learned mental models.
Meanwhile, research in cognitive aesthetics suggests that certain visual structures have innate appeal across human populations (Ramachandran & Hirstein, 1999 10). Interestingly, some of these structures resemble patterns produced by Reaction-Diffusion systems—a connection proposed here as a possible explanation for their cross-cultural resonance.
Rather than cultural borrowing alone, these recurring forms may reflect a collective human response to the visual logic of the natural world. We recognize symmetry, flow, and rhythm not only because we’re taught to, but possibly because our perceptual systems are tuned to detect them. Reaction-Diffusion systems mirror this logic: simple natural processes generating complex, yet familiar, visuals. The similarity between these algorithmic patterns and traditional motifs hints that we may all be drawing from the same source—nature itself.
| Example | Object | Culture/Period |
|---|---|---|
 |
High-rimmed bowl. | Greece/Late Geometric |
 |
Krater. Burial chamber 112. | Spain/Iron Age |
 |
Xicalcoliuhqui. Mosaic from the palace in Mitla, Mexico, Oaxaca | Mexico/pre-Columbian |
Figure 8 The wave/spiral/meander motif around the world
Consider, for instance, the recurring spiral motif found in various ancient cultures; it often embodies concepts of growth, cycles, or spiritual journeys, thereby functioning as a visual mnemonic that transmits collective narratives and ancestral knowledge across generations. This suggests that the very structure and repetition of folk motifs serve as active mechanisms for cultural memory, mirroring the iterative processes seen in algorithmic pattern generation.
While the mirroring of natural forms in folk motifs is a well-established observation (Glassie, 199911), the striking reappearance of these forms through algorithmic generation, independent of direct observation, suggests a deeper connection. This phenomenon implies that such patterns may not solely be products of cultural transmission but rather emergent properties of underlying natural laws or generative systems—whether biological or computational (Johnson, 200112).
This perspective introduces the concept of ‘algorithmic archaeology,’ where we engage not in uncovering historical memory in the traditional sense, but rather in a process of computational generation that resonates with culturally familiar forms. Through RD systems, we propose a method to computationally rediscover visual archetypes that may have been perceived by our ancestors, potentially reflecting an inherent human sensitivity to the ‘invisible script’ of nature’s generative principles (Arnheim, 197413).
By “algorithmic archaeology,” we mean the process of uncovering visual forms that feel culturally familiar—despite being generated by natural algorithms. This is a conceptual proposal rather than an empirically proven method: it suggests that shared perceptual responses to natural patterns might explain why certain motifs recur across cultures, but it does not claim definitive evidence of historical memory.
What if our traditions are less about invention and more about resonance—with the same forces that shape animal skin, cloud formations, and coral? Reaction-Diffusion systems make that visible. By watching code mimic nature, and culture mimic nature, we realize they’re not separate threads. They’re one loop: patterns in nature, patterns in code, patterns in us.




Figure 9: Geometrized floral motifs produced with a RD inspired algorithm
By exploring the algorithmic underpinnings of folk motifs through Reaction-Diffusion systems, this work offers a novel lens to appreciate the profound continuities between nature’s generative principles, the logic of code, and the enduring patterns embedded within human cultural memory.
We implemented the Gray–Scott model on a 100x100 grid using a nine-point (Moore) neighborhood. We denote chemical concentrations by \(a,b\), diffusion coefficients by dA, dB, feed rate by \(\text{feed}\), and kill rate by \(k\).
In our implementation, we adopt a weighted Moore neighborhood stencil: the central cell has weight \(w_c = -1\), the four orthogonal neighbours weight \(w_o = 0.2\), and the four diagonal neighbours weight \(w_d = 0.05\):
\[ \begin{matrix} 0.05 & 0.2 & 0.05 \\ 0.2 & -1 & 0.2 \\ 0.05 & 0.2 & 0.05 \end{matrix} \]
At each time step and grid cell \((x,y)\), we compute the new concentrations via Euler integration:
// compute discrete Laplacian for a and b:
LapA = laplaceA(x, y); // sum of neighbor a's - 8 * a[x][y]
LapB = laplaceB(x, y); // sum of neighbor b's - 8 * b[x][y]
next[x][y].a = a + (dA * LapA) - (a * b * b) + (feed * (1 - a));
next[x][y].b = b + (dB * LapB) + (a * b * b) - ((feed + k) * b);We explore three initialization methods for \(b\) to control pattern emergence:
Randomized Start:
Central Square Seed:
Central Perturbation:
General Perturbation:
| Figure Series | dA | dB | feed | k | Seeding |
|---|---|---|---|---|---|
| 1 | 1.0 | 0.5 | 0.055 | 0.062 | Randomized start 10x10 |
| 4 | 1.0 | 0.5 | 0.055 | 0.062 | Central square 10x10 |
| 2 | 1.0 | 0.5 | 0.0255 | 0.0557 | Central perturbation 2x2 |
| 3 | 1.0 | 0.5 | 0.0365 | 0.061 | General perturbation |
| 5 | 1.0 | 0.5 | 0.032 | 0.0062 | Central square seed 10x10 |
| 6 (ChaosMods) | 0.12 | 0.09 | 0.035 | 0.065 | Central square seed 10x10 |
| 7 (ChaosMods) | 1.3 | 1.54 | 0.0255 | 0.062 | Central square seed 10x10 |
| 9 (ChaosMods) | 1.3 | 1.55 | 0.0055 | 0.0062 | Central square seed 10x10 |
Chaos Mods:
To produce the patterns seen in Figure 7, we altered the Gray–Scott model by modifying the depletion term of the equation:
next[x][y].b = b + (dB * laplaceB(x, y)) + (a * b * b) - ((k + feed) * a);This adjustment replaces the standard \(-((k + {feed}) * b)\) decay term with \(-((k + feed) * a)\), making the removal of \(b\) dependent on the presence of \(a\). This breaks the usual symmetry and destabilizes the feedback loop, resulting in unpredictable, chaotic morphologies. This intentional symmetry-breaking is used to increase pattern diversity and explore a wider range of emergent forms.
To produce patterns seen in Figure 6 and Figure 9, we used other variations that perturb the update rule for \(a\), replacing the standard feed term with \((\text{feed} + f)(1 - b)\). Unlike the usual Gray–Scott term, which biases toward replenishing \(a\) when it’s depleted, this version drives \(a\) in proportion to the absence of \(b\), amplifying chaotic feedback where \(b\) is low and intensifying spatial contrast.
Alan M. Turing, “The Chemical Basis of Morphogenesis,” Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 237, no. 641 (1952): 37–72. https://doi.org/10.1098/rstb.1952.0012.↩︎
Code written in p5.js by Nicu Popescu↩︎
Alan M. Turing, “The Chemical Basis of Morphogenesis,” Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 237, no. 641 (1952): 37–72. https://doi.org/10.1098/rstb.1952.0012.↩︎
John E. Pearson, “Complex Patterns in a Simple System,” Science 261, no. 5090 (1991): 189–91. https://doi.org/10.1126/science.261.5118.189.↩︎
Code written in p5.js by Nicu Popescu↩︎
Code written in p5.js by Nicu Popescu↩︎
Code written in p5.js by Nicu Popescu↩︎
Lidwell, W., Holden, K., & Butler, J. (2010). Universal Principles of Design. Rockport Publishers. https://books.google.ro/books/about/Universal_Principles_of_Design_Revised_a.html?id=l0QPECGQySYC&redir_esc=y↩︎
Gombrich, E. H. (1960). Art and Illusion: A Study in the Psychology of Pictorial Representation. Princeton University Press. https://archive.org/details/artillusionstud00gomb↩︎
Ramachandran, V. S., & Hirstein, W. (1999). The Science of Art: A Neurological Theory of Aesthetic Experience. Journal of Consciousness Studies, 6(6-7), 15-51. https://philarchive.org/rec/RAMTSO-5↩︎
Glassie, H. (1999). Material Culture. Indiana University Press. https://books.google.com/books/about/Material_Culture.html?id=h0coAQAAMAAJ↩︎
Johnson, S. (2001). Emergence: The Connected Lives of Ants, Brains, Cities, and Software. Scribner.↩︎
Arnheim, R. (1974). Art and Visual Perception: A Psychology of the Creative Eye. University of California Press. https://archive.org/details/art-and-visual-perception-rudolf-arnheim↩︎