Pulse, Pattern, Permutation: Applying Schillinger’s Pulse Interference in Computer-Assisted Composition

Introduction

The pursuit of models for rhythmic pattern generation constitutes a fundamental element of computer-assisted and algorithmic music composition domains. Various processes have been developed to achieve rhythmic diversity while maintaining musicality and consistency. These processes utilise a variety of mathematical, stochastic and biologically inspired methods to create structured or evolving patterns. For example, Genetic algorithms (GAs) evolve rhythmic populations using fitness criterion ^{1 2}. Stochastic and Markovian Processes use probability distributions for randomised note durations and harmonic progressions, often combined with rhythmic patterns ^{3 4 5}. Broadly, these processes aim to break free from habitual patterns of rhythmic arrangements in search of flexible and novel structures.

In this paper, we discuss one approach based on the mathematical pattern generation found in the historical work by Joseph Schillinger - “The Schillinger System of Musical Composition”⁶, which was developed and taught throughout the United States during the 1940s. Schillinger’s system was developed to build a definitive study on the relationship of numbers to music. The system uses permutations, combinations, trigonometric functions, geometric patterns and other mathematical processes to analyse and generate rhythms, melodies, harmonies and even entire compositions algorithmically (see ^{7 8 9} for detailed analyses and application of The Schillinger System of Musical Composition, including its principles such as permutation, interference and pitch symmetry). “The basic philosophy of the Schillinger approach is to help solve musical problems with the mathematical approach, addressing many of the limitations of conventional music theory”¹⁰. For Schillinger, conventional music theory often privileged Western tonal-harmonic models, however he proposed mathematical processes that allow composers to systematically generate material outside of those boundaries. In this sense, he saw his system as providing alternatives to habitual approaches, offering procedural solutions for rhythmic complexity, polymodality and structured yet flexible pattern-making.

Applying Schillinger’s System

We demonstrate the application of Schillinger’s pulse interference of integers to create rhythmic patterns, with the algebraic expansion of integer combinations generating a variety of musical note placements within a sequence. The central idea involves combining different rhythmic cycles to produce complex polymeters and syncopations. Additionally, the same system is applied to the generation of musical intervals to create ‘modal’ scale forms, and the combination of these with rhythmic patterns results in shifting harmonic layers within the sequence.

Fundamentally, Schillinger’s theory of rhythm is based on combining two or more pulses with different frequencies starting at the same time. He calls this “interference” and uses series of integers to calculate the resulting rhythmic patterns. These numbers represent time durations between pulses. Pulse combinations create varying rhythmic results, including strong pulses when they coincide. Another method described by Schillinger involves mathematical manipulation of the master time signature, where time signatures are divided into whole-number parts that sum to the original value. Schillinger’s method divides the time signature into two parts, like 5 becoming (1+4) or (2+3), avoiding equal parts for even numbers like 4. These parts are then rotated (a,b) to (b,a) and combined (“interference”) to create new, larger sub-groups. This process can be iterated until the sub-group is entirely composed of 1s (uniformity). The method then involves the squaring of the sub-grouped master time signature fragments to derive a new interference pattern.

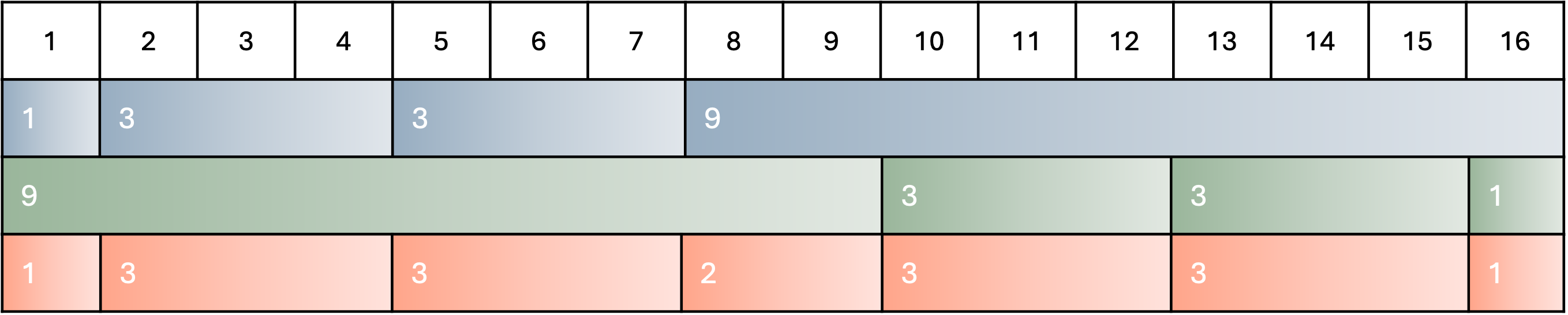
In our first example, a time signature of 4/4 is broken into a subgroup of 3+1 (and 1+3). This is then squared. (a+b)² creates the equation a² + a.b + b.a + b², which gives us 9+3+3+1 (and 1+3+3+9). When applied to a 16 beat sequence of note durations, the interference of the two patterns creates a further rhythmic pulse 1, 3, 3, 2, 3, 3, 1 (see figure 1).

The expanded version of a² + a.b + b.a + b² is a(a+b)+b(a+b) and results in a 12+4 subgroup for another rhythm (see figure 2).

To create more variety in the pattern generation, the time signature of 5/4 is superimposed as the squared subgroup (3+2)² or 9+6+6+4 for a further note timing pattern (see figure 3).

Squaring the larger integer of 5/4 creates an interference pattern between the numbers of 4+1+3+1+1+2+1+2+1+1+3+1+4 for another pulse (see figure 4), and a final note pattern is generated using the meter of 3/4 (2+1), which expands to 4+2+2+1 (see figure 5).

Applying the idea of rhythmic pattern generation to pitch intervals results in a variety of scales or modes¹¹. For example, a musical octave of 12 chromatic intervals can be subgrouped into number combinations of 7+5 and 5+7. The basic rhythm interference pattern generated by a rhythm of 7 followed by 5, against 5 followed by 7, produces the numbers 5, 2, 5, which creates permutations of 5+2+5, 5+5+2 and 2+5+5. These trinomial patterns can then produce quintinomial permutations by further breaking up the 5 term into 2+3 or 3+2:

1. 2+3+2+3+2
2. 3+2+3+2+2
3. 2+3+2+2+3
4. 3+2+2+3+2
5. 2+2+3+2+3

When these patterns are applied to semitone intervals from the root note of C, for example, they result in the following 5-note scales (see figure 6): 1. C, D, F, G, Bb, C - mode of Bb major pentatonic 2. C, Eb, F, Ab, Bb, C - natural minor or mode of Ab major pentatonic 3. C, D, F, G, A, C - mode of F major pentatonic 4. C, Eb, F, G, Bb, C - mode of Eb major pentatonic 5. C, D, E, G, A, C - C major pentatonic

While these scales exhibit distinct characteristics, they are fundamentally related by virtue of a common derivation schema. In our implementation, these scales can be loaded in real-time whilst the sequence plays to create musical contrast, as is evident within the video examples below.

Implementation and Results/Examples

The algebraic outputs derived from the Schillinger System of Musical Composition have been implemented within a Pure Data (Pd) environment as a custom software patch (see figure 7). This patch is designed to translate the abstract mathematical relationships generated by the Schillinger techniques into concrete musical data in the form of MIDI note messages, allowing a direct sonic realisation of complex compositional structures conceived through algebraic principles. Additionally, the patch includes a feature that enables the real-time selection of various modal outputs as the musical piece unfolds. The addition of this interactive element provides a layer of dynamic control, enabling and encouraging shifts in the harmonic and melodic character of the generated music according to the performer’s aesthetic decisions in real-time. This ability to select different modal frameworks on the fly introduces an improvisational element, moving beyond a purely pre-determined outcome from the initial algebraic generation. The Pure Data patch is then connected via MIDI to an iPad running Audio Unit Mixer (AUM) containing various software synthesisers. This combination of custom software and modern mobile music-making platforms provides a rich environment for exploring novel sonic territories and compositional possibilities rooted in the theoretical framework of the Schillinger System.

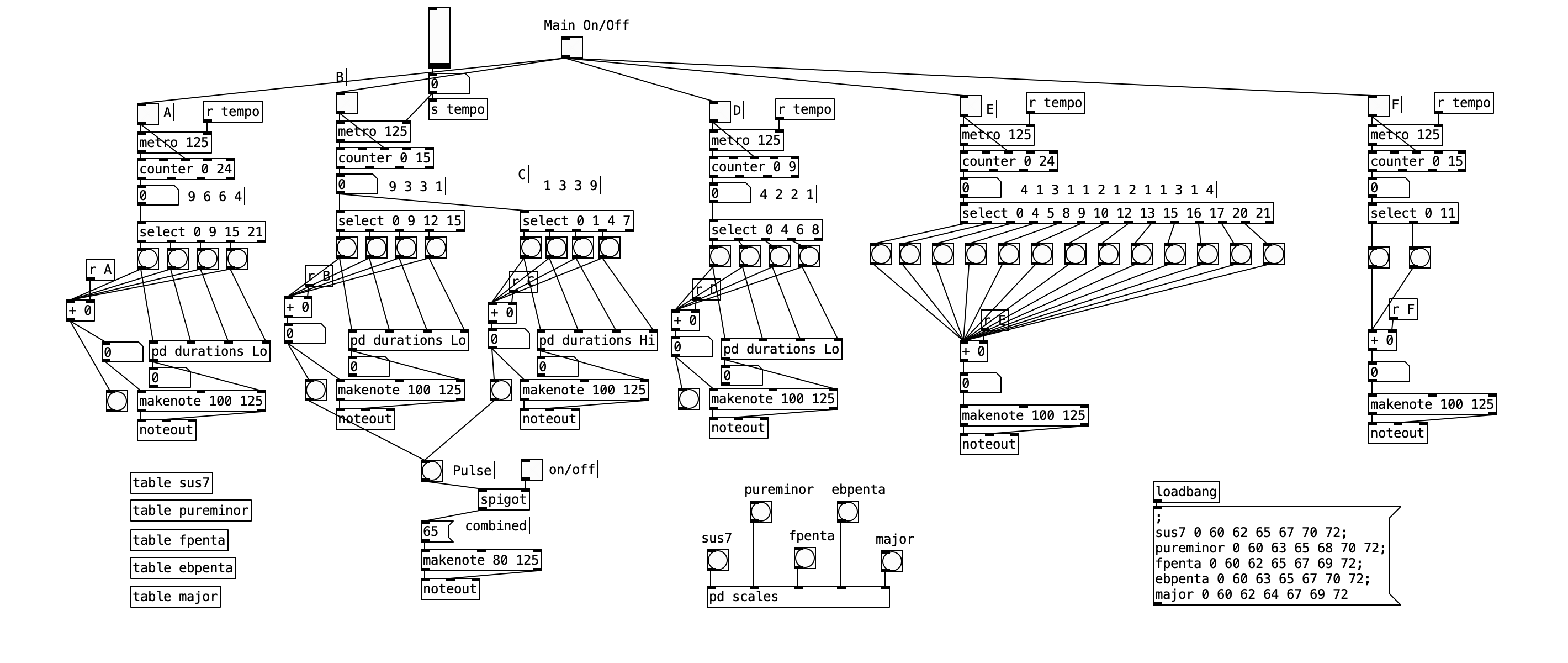
To illustrate the algebraic generation of rhythmic patterns, the basic 4/4 subgroup derivations of 1, 3, 3, 9 and its retrograde are applied to percussive sounds (see figure 8), with the addition of the expanded subgroup of 12+4, and finally an entire rhythm pattern is displayed, utlising all the algebraic rhythms discussed.

Another example (see figure 9) highlights these rhythms as applied to a synthesiser patch, with a selection of generated interval modes being applied to create harmonic motion and illustrate the basis of a creative process with these concepts.

Figure 10 demonstrates the processes applied to a sustained sound, in this case a string orchestral section, where the harmonic layering is more evident when switching scale modes.

Finally, figure 11 demonstrates a creative ambient integration, consisting of both sustained and percussive sounds, again with harmonic variation applied by switching between the various modes.

While the patch was initially conceived as a compositional aid, its ability to switch scales and rhythmic groupings in real time makes it well-suited for live performance. This opens space for improvisation, where performers can actively shape harmonic and rhythmic direction on stage. In practice, the software operates as both a compositional sketch generator and as a performance tool.

Conclusion

Schillinger designed his system to aid the creative process, not replace it, and the outcomes from his techniques can be translated into musical forms by the composer. The process of integer interference and algebraic expansion to generate rhythmic patterns and modal scales is relatively straightforward and does not require deep understanding of mathematics. This makes the system accessible to most composers. The software implementation of the system offers further simplification of the process, allowing a composer to easily audition the results of many arrangements of pulse interferences relatively quickly and apply their own aesthetic preferences in service of their compositions.

Being a strictly mathematical process ensures the outputs have a structure and completeness within themselves - there is an inherent cohesion due to the number relationships. For the listener, this often translates as perceivable consistency in phrasing or repetition, even when the surface-level rhythm or harmony is complex. Musicality here is not assumed to mean tonal consonance, but rather the sense of patterned organisation and recognisability that emerges from number relationships. While this paper demonstrates only a small component of the Schillinger system, it highlights this inherent musicality from a pattern-based approach and its potential usefulness for composers, especially to inspire new musical directions as a contrast to traditional musical theory approaches.

In choosing to focus specifically on Schillinger’s procedures, we do not advocate for strict adherence to the “system” as a totalising method. Instead, we see value in revisiting one historically significant framework as a way of highlighting how mathematical approaches can serve creativity. In practice, these same procedures could easily be combined with alternative algorithmic or other diverse strategies. Our emphasis on Schillinger is less about fidelity to his system and more about recontextualising a historically situated idea for contemporary composition and performance practice.