Published September 2025 as part of the proceedings of the first Alpaca conference on Algorithmic Patterns in the Creative Arts, according to the Creative Commons Attribution license. Copyright remains with the authors.
doi:10.5281/zenodo.17084394
Fractal artists have been constructing patterns by choosing specific sequences of locations in deep Mandelbrot set zooms for at least 25 years. But when the aim is to design fractal patterns, there are more direct ways to go about it that offer immediate interactive feedback and greatly reduced computational expense. Inflector Gadget is a tool to make creating Julia morphing patterns simple and fun, allowing artists to focus on pattern design.
Sculpting patterns out of embedded Julia sets in deep Mandelbrot set zooms by careful choice of when and where to “go off-centre” and choose a new zoom focus goes back to the 1990s1. By early 2010s, newly popular algorithms using perturbation and series approximation techniques greatly reduced the computational difficulty of generating deep zoom images2. Previously, render times using Fractal Extreme could be several weeks3, which reduced to several minutes using Kalle’s Fraktaler 2 or MandelMachine.
This allowed artists to generate more complex fractal artworks, as each next step in Julia morphing typically needs half as much zooming again as the total zoom of the previous step. Render times could still eventually be weeks, but now with much higher image resolution and more finely resolved structures.
The only difficulty present is that those shapes lie at ridiculous depths. Since perturbation, the patience required to perform the actual zooming exceeds the patience required to sit trough the render time. – DinkydauSet, 20144.
In March 2016, the popular fractal exploration software Kalle’s Fraktaler 2 version 2.9.3 added the Newton-Raphson zooming feature, which allows automatically zooming to a baby Mandelbrot set or its embedded Julia sets5. This reduced the boring labour of manually zooming, allowing artists to focus on pattern construction.
But even as early as 2014-2015, fractal artists like stardust4ever, Fractal Universe and DinkydauSet were thinking of alternatives to deep Mandelbrot zooming, to make engaging fractal artworks with less computational cost:
Just contort the set to produce whatever feature you want to create, then render just that, rather than brute force the pattern by relentless zooming. – stardust4ever, 2014.6
In August 2014, Kalle’s Fraktaler added the “Show Inflection” feature, which gives a preview of what the image will look like when zooming in to a particular point in the Mandelbrot set7. The name “inflection” for the plane transformation was coined by stardust4ever.
Fractal Universe discovered that the commercial software Ultra Fractal 5 could be programmed to simulate or model the shapes it would be possible to construct in exceedingly deep Mandelbrot set zooms.
This is a great idea. I didn’t know this was possible with ultra fractal. Plane transformations combined with a simple julia set renderer is all that’s required. Thanks for finding this possibility. I will definitely use it to make some “models”. Unfortunately it’s a little hard to use. It could be as easy as a single click (add julia transformation centered at the pixel clicked at) but it doesn’t look like that’s possible, so it takes many clicks to perform a morphing. – DinkydauSet, comment on YouTube video by Fractal Universe, 8 years ago (as of April 2025)8.
In January 2017, DinkydauSet published a high resolution image modelling a combination of five patterns (some of which were compound patterns), that would be found in the Mandelbrot set with minimum zoom depth around 101012, which is vastly beyond current computational capabilities9.
In February 2017, I started my project Inflector Gadget, which does what DinkydauSet suggested: a single click to add an inflection point10.
In January 2018, Dinkydau published Explore Fractals11:
I used [Inflector Gadget] and I wanted more possibilities and the kind of coloring that I normally use. – Dinkydau, 202012
Initially a desktop application written in C++, for Linux and Windows, using OpenGL 4 GLSL shaders, in March 2025 I ported Inflector Gadget to JavaScript and WebGL 2 with OpenGL ES 3 shaders13. Running inside a web browser avoids the need to compile for different operating systems, and sidesteps the security implications of distributing compiled executables. The generated patterns (in an editable state) can also be bookmarked or shared by copy-pasting URLs.
In May 2024, Isaac Hew published some deep Mandelbrot set zoom simulations, which unlike Inflector Gadget’s and Dinkydau’s Explore Fractals’ images, and Fractal Universe’s video, contain the dense rings of decorations that are found in real Mandelbrot set zooms 14 15 16. He has not published his method.
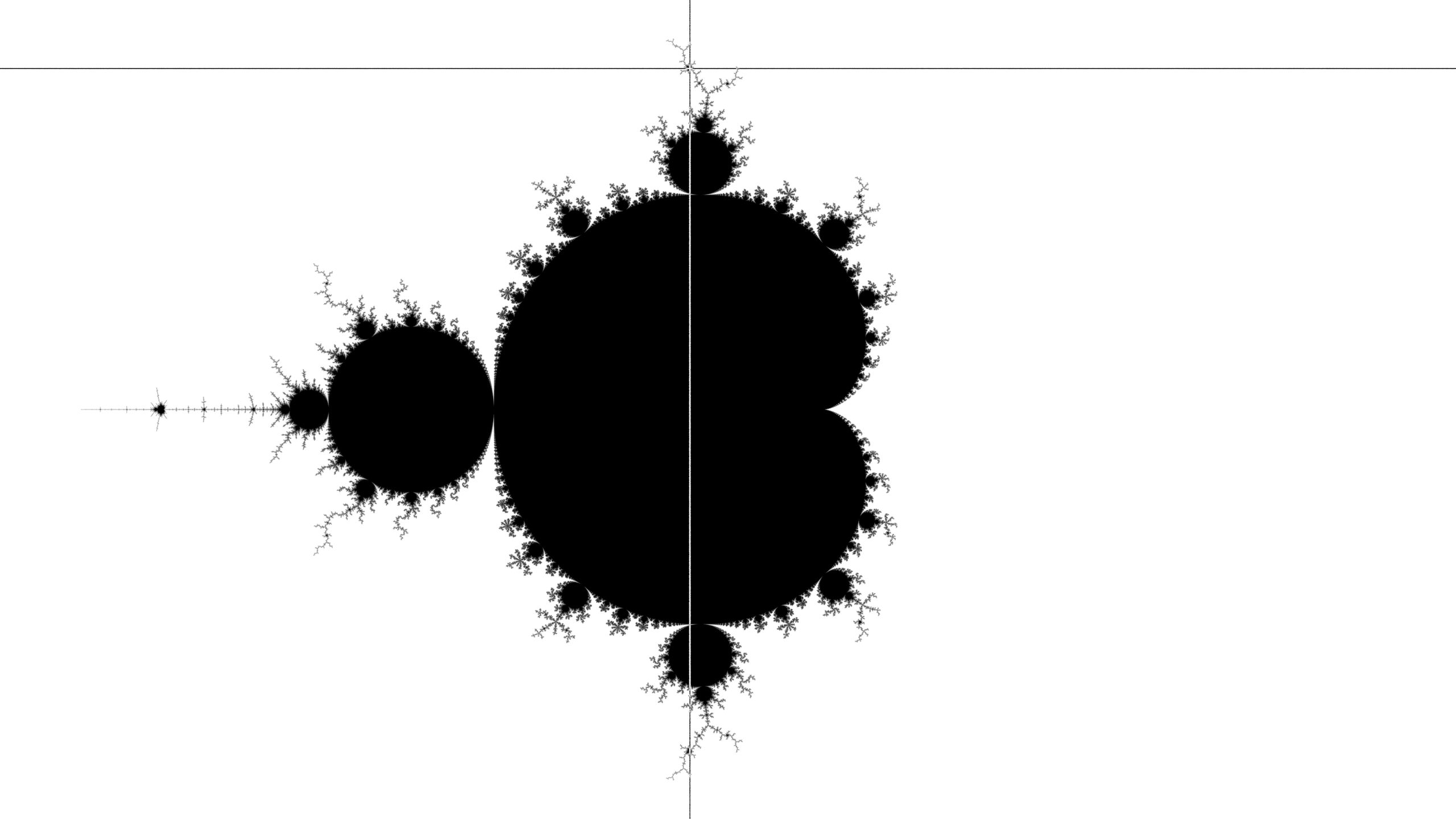
When opening Inflector Gadget, a view of the Mandelbrot set is shown. Clicking on the image at a particular point shows the corresponding Julia set.
The Mandelbrot set has a structure built of attractors of different integer periods. The main cardioid has period 1, the biggest disk on the left has period 2, and the next biggest disks at top and bottom have period 3. This structure is reflected in the shapes of the Julia sets, for example a Julia set near a period 3 disk has a branching shape with 3 arms.
If the initial point is inside the Mandelbrot set, the Julia set will have solid regions. Too little solid can be hard to work with, as subsequent morphs tend to make the shape turn to dust. Too much solid can also be awkward, so it can be advantageous to select the initial point to be inside a baby Mandelbrot set. This will give a Julia set with solid nodes connected by filaments, whose character depends on the location of the baby Mandelbrot set within the whole.
Subsequent clicks wrap the current pattern two-fold around the clicked point, allowing shapes to be sculpted17. The period of the Julia set suggests the number of patterns that can be combined in a natural way: clicking in the shortest arm of the primary spiral brings the click position to the origin and wraps the shape twice, which has the effect of rotating the spiral one step. The new shortest arm can be inflected in a similar way, until after period-many steps the first inflection is back in the shortest arm position.
Where to click within the shortest arm at each stage is the main artistic decision in designing the final fractal image. For example, a tree can be constructed by picking a node to the side of the central node (of the shortest spiral arm), a line can be constructed by picking a node further out from the center of the whole shape, or a large disk can be formed by clicking inside the central node itself.
To get a regular shape, the steps should be repeated in a regular way each time each sub-pattern gets back to the shortest arm position. This can mean manually counting filament branches and nodes, using the navigation tools to zoom in to choose more accurately.
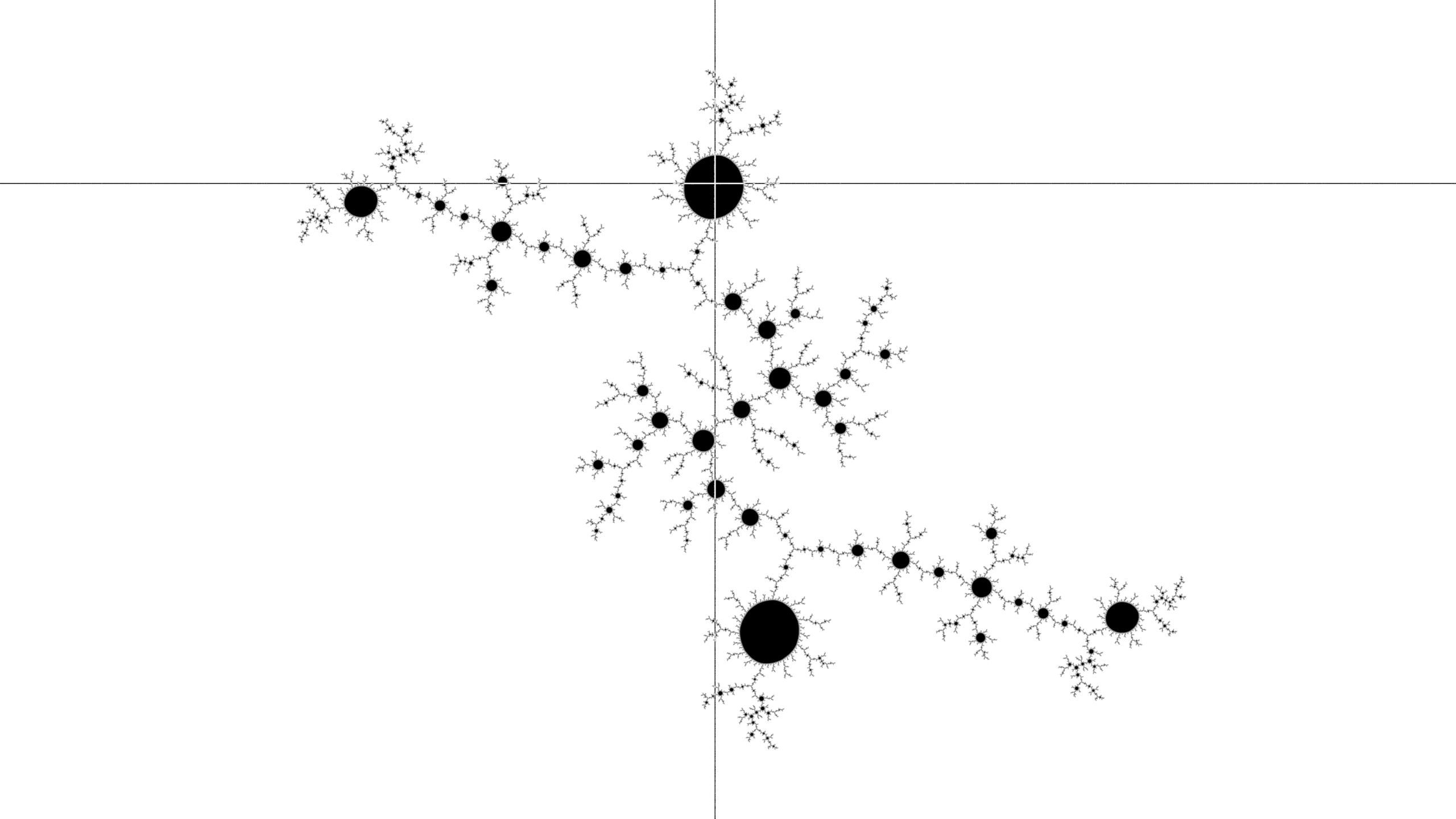
In the following images, the position of the next click is marked with a cross-hair. To make a shape with three patterns, start by clicking near the period 3 disk at the top of the Mandelbrot set (the bottom disk also has period 3, as does the largest baby Mandelbrot set in the antenna on the left).

The corresponding Julia set is then shown. This one has solid nodes because the initial click was in a baby Mandelbrot set. The shortest arm is on the top right. Start to form a tree by clicking to the side of the main node in the shortest arm.
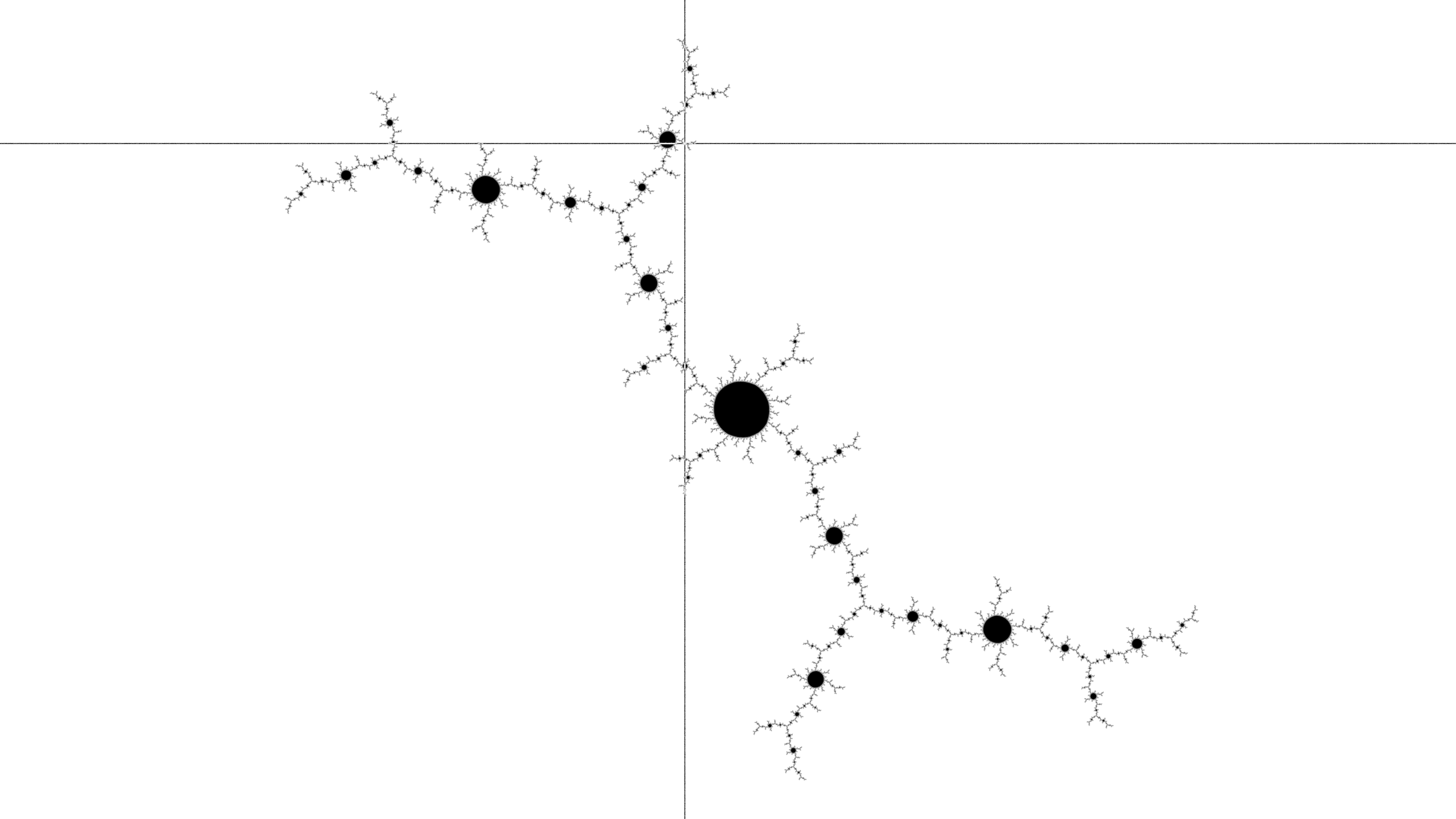
The previous click point has now moved to the center of the image, with two-fold rotational symmetry. Start to form a disk by clicking in the main node of the shortest arm.
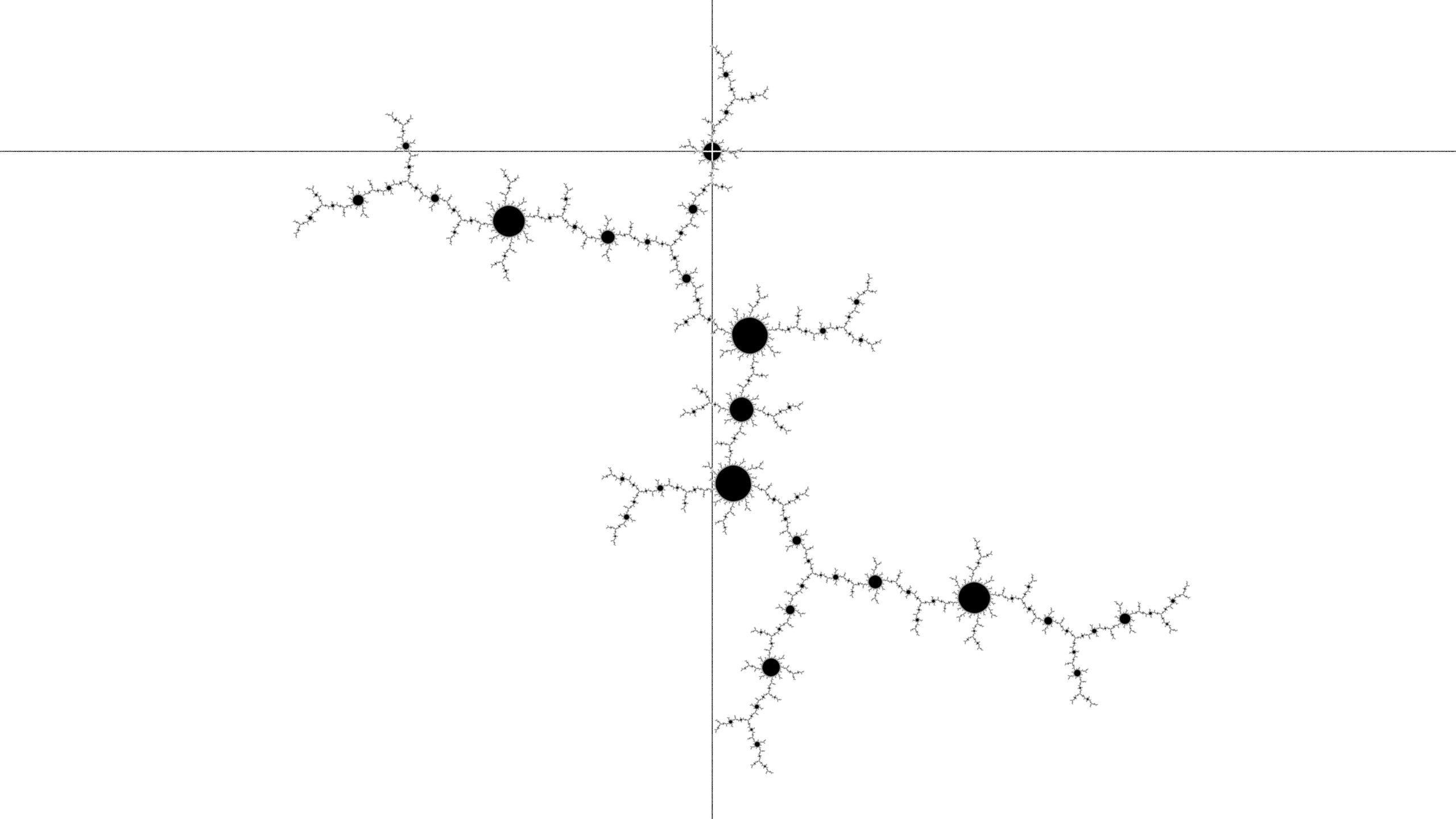
Again, the disk is now in the center of the image, and the previous center has rotated clockwise around the spiral arm. The shortest arm is now in the third phase (of three) of the pattern construction - start to form a line by clicking beyond the main node of the shortest arm.
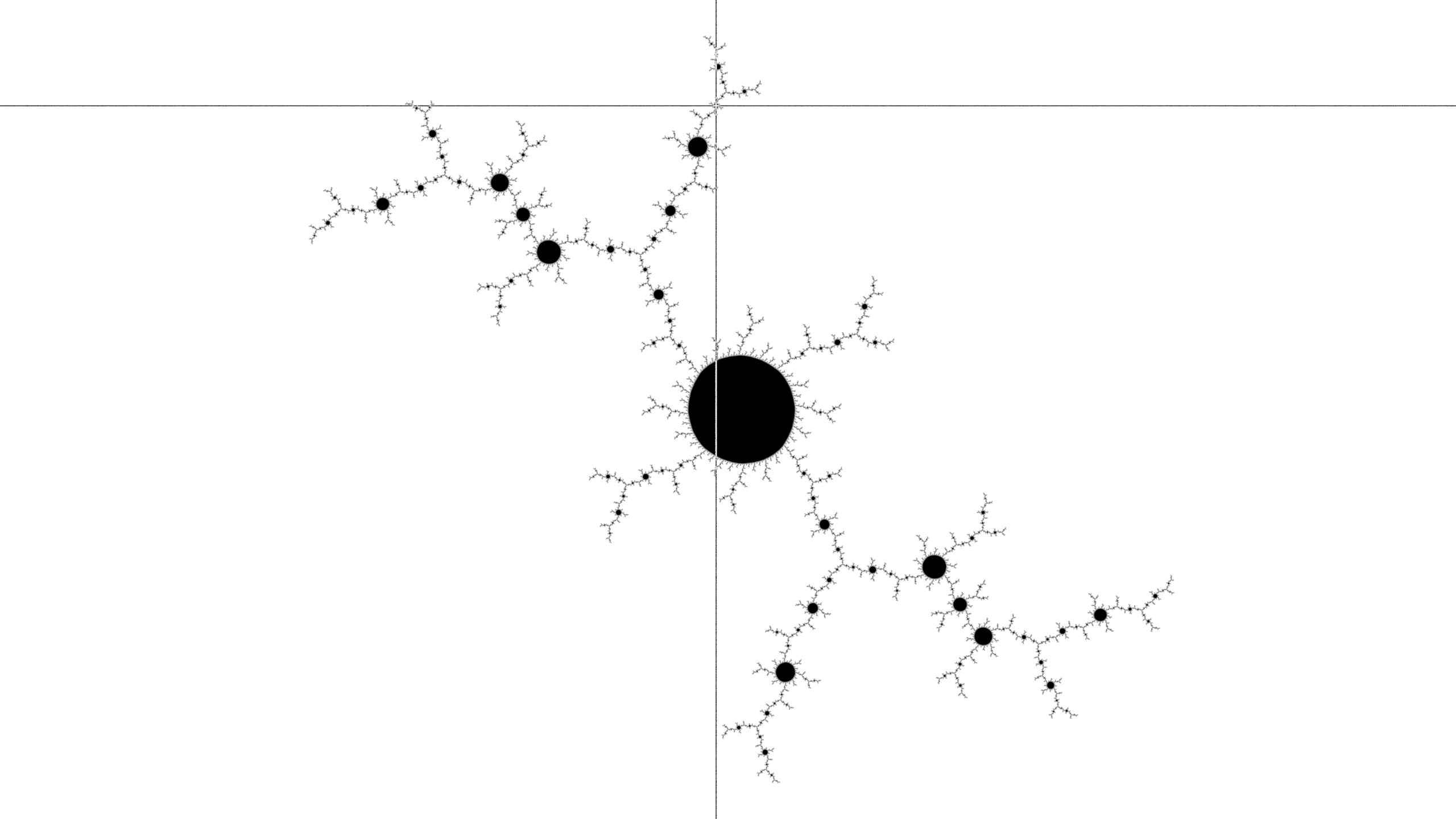
The pattern from three steps ago has now returned to the shortest arm position. The following clicks no longer require deep decision-making, rather the shapes appearing in the shortest arm naturally guide the artist to continue constructing the motif that has been started.
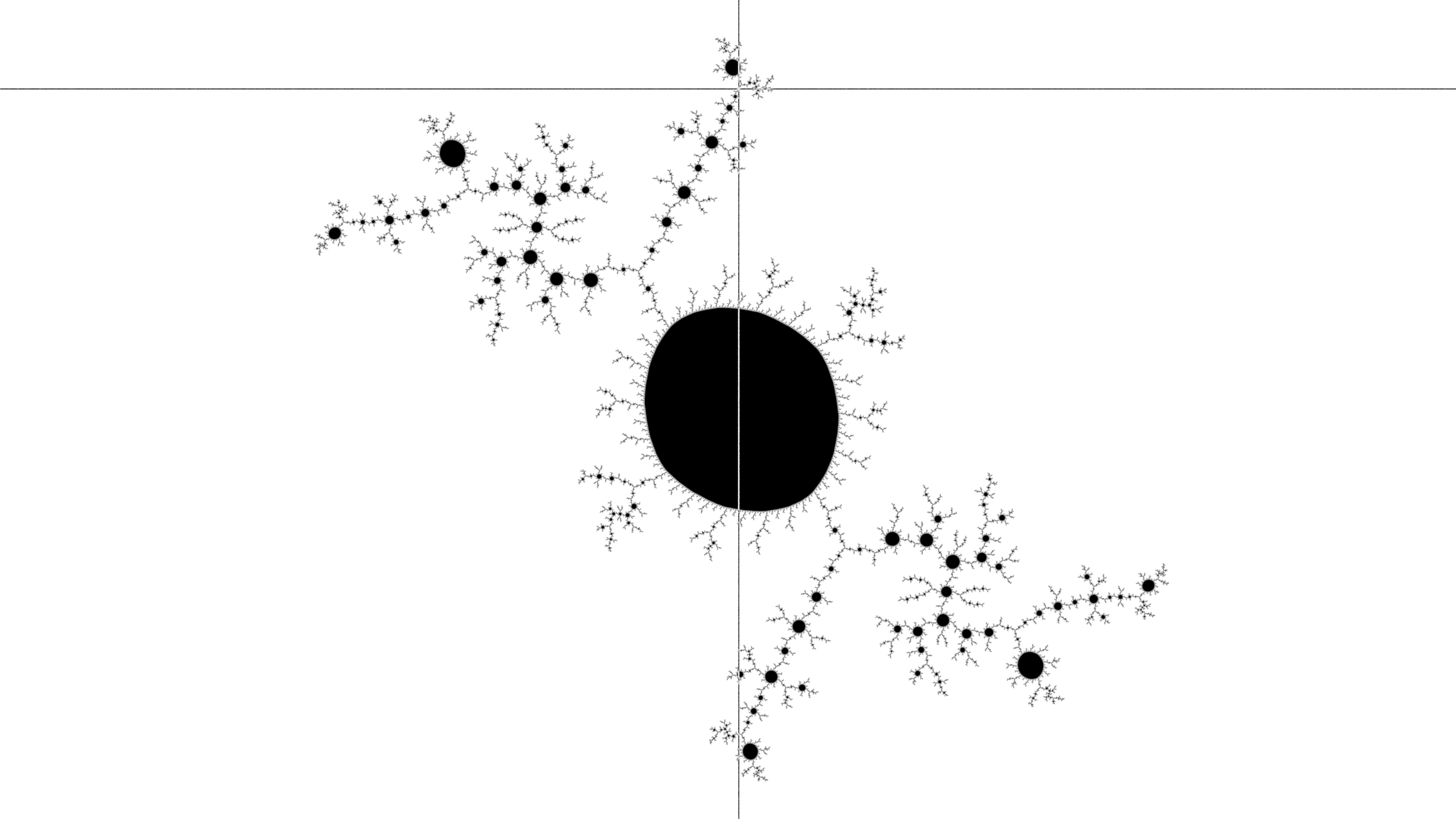
Thus, continue to make the tree by clicking to the side of the main node.
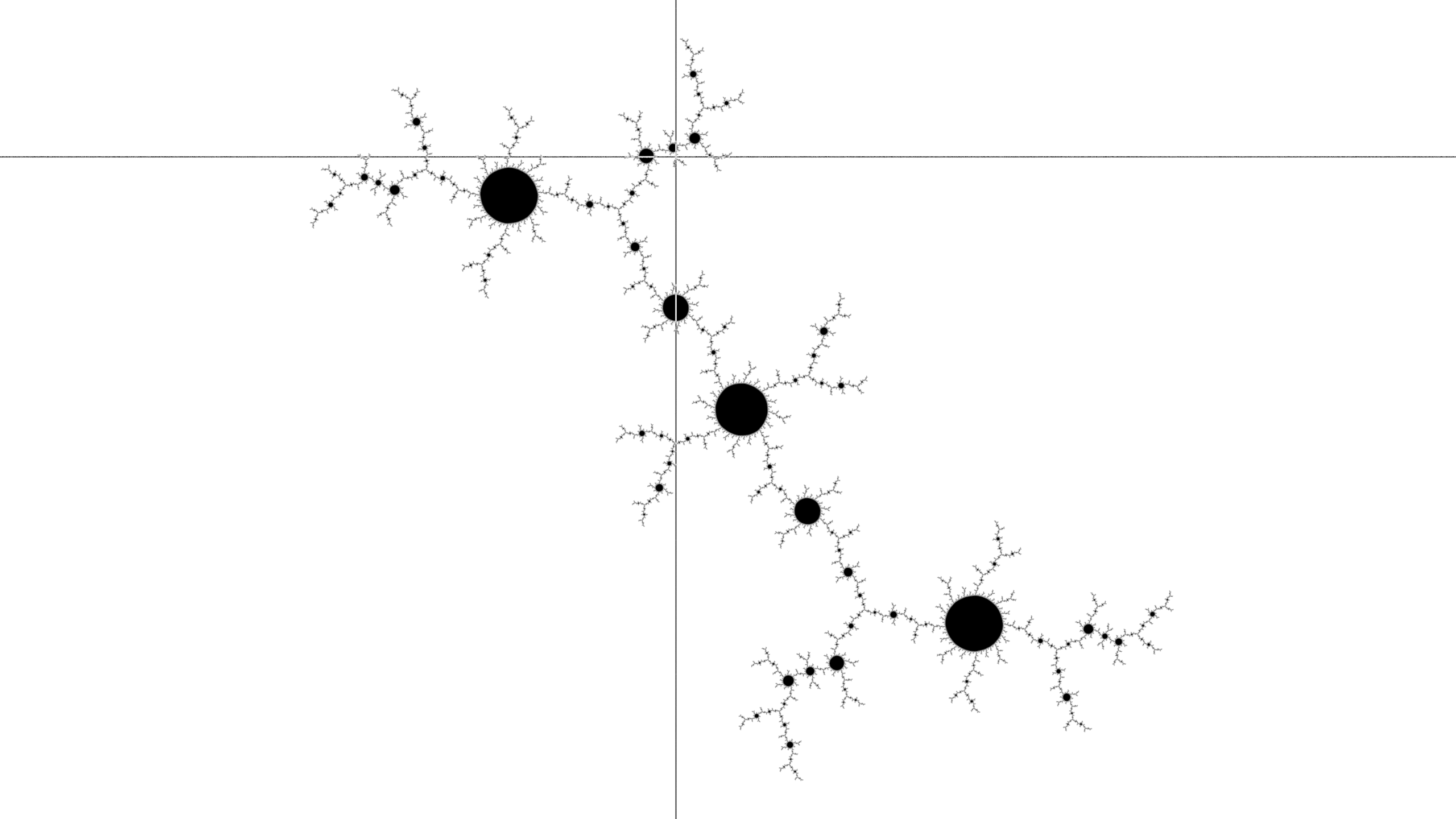
Contine to make the disk.
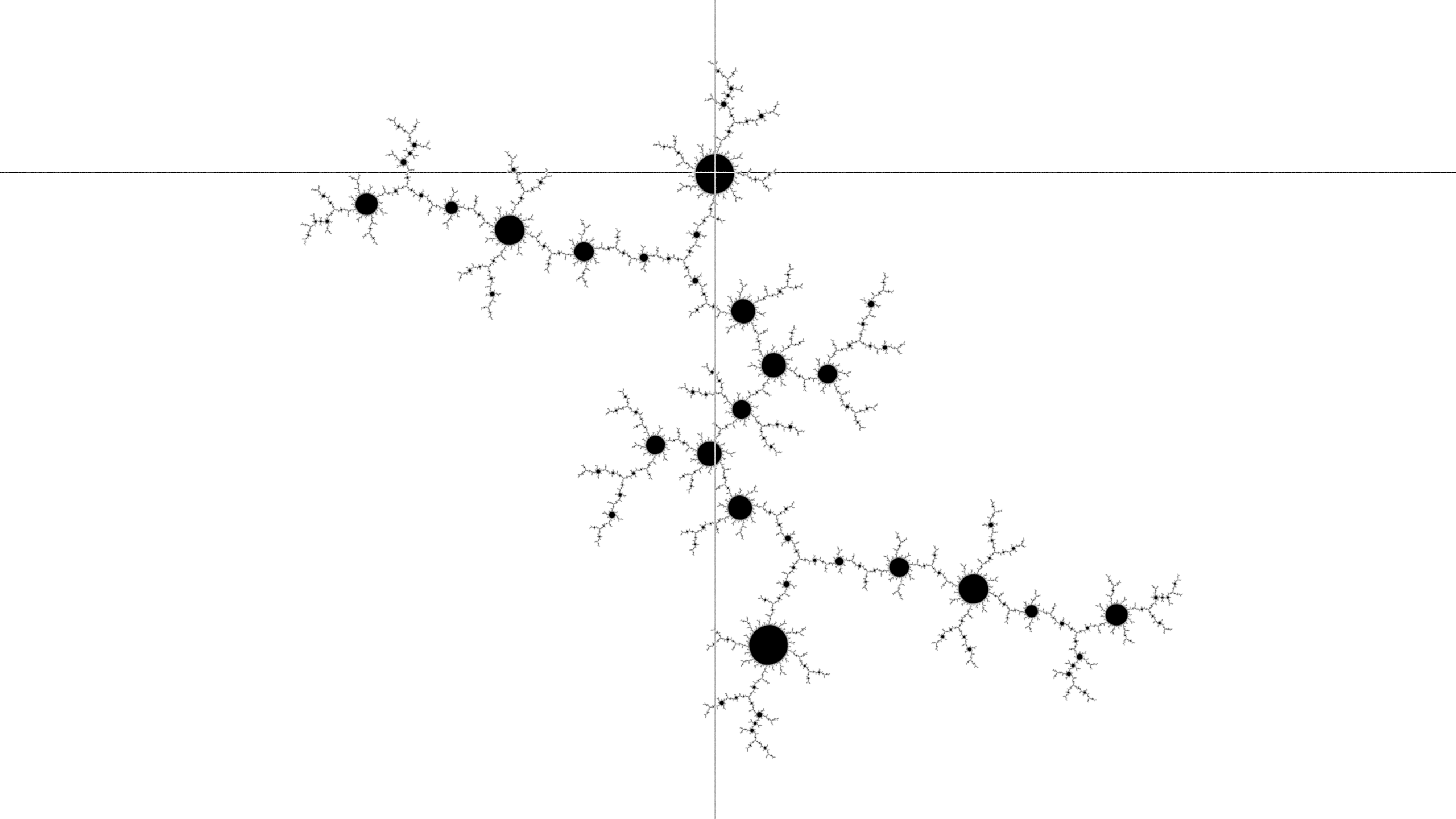
Continue to make the line.
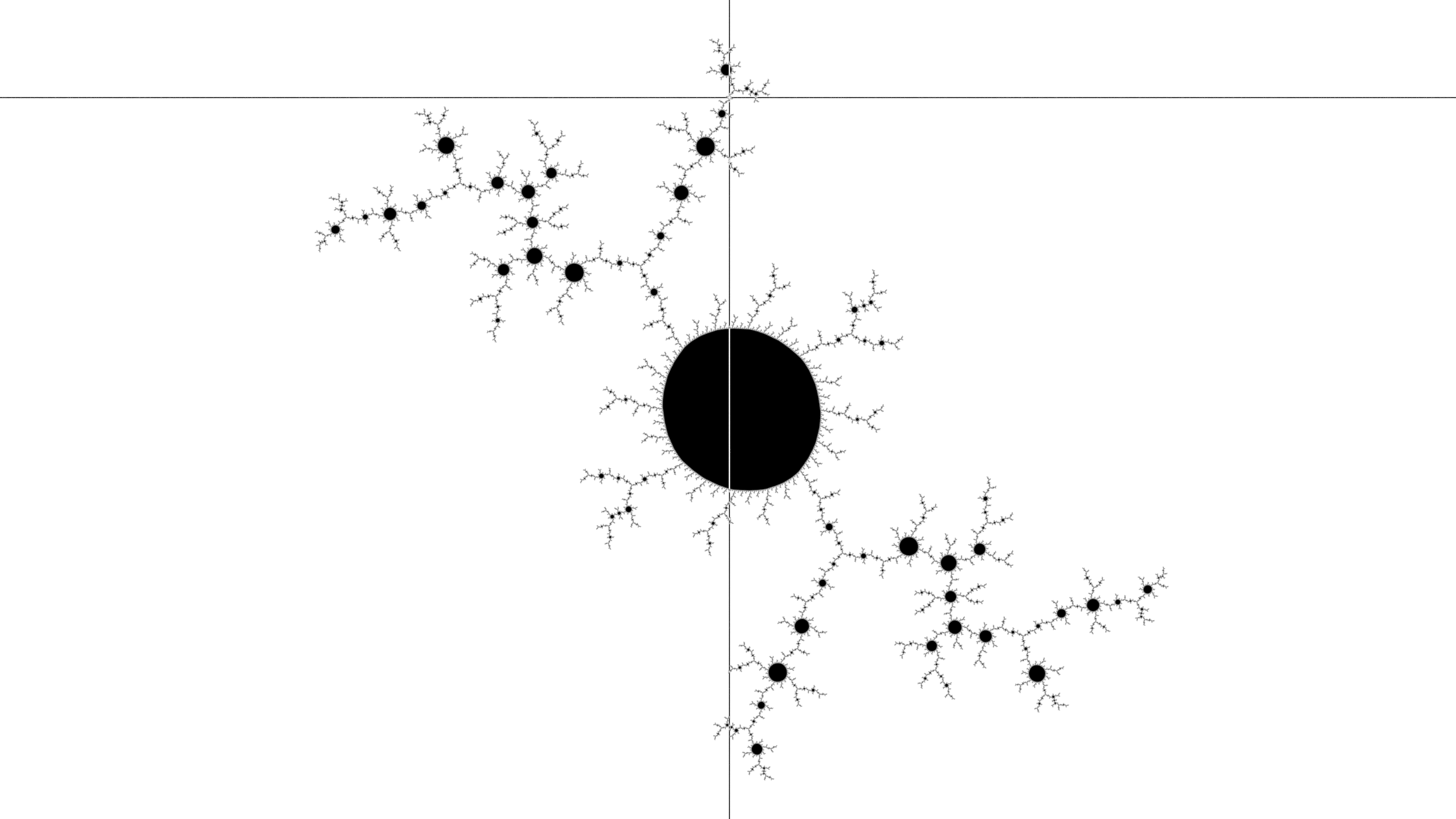
Continue to make the tree.
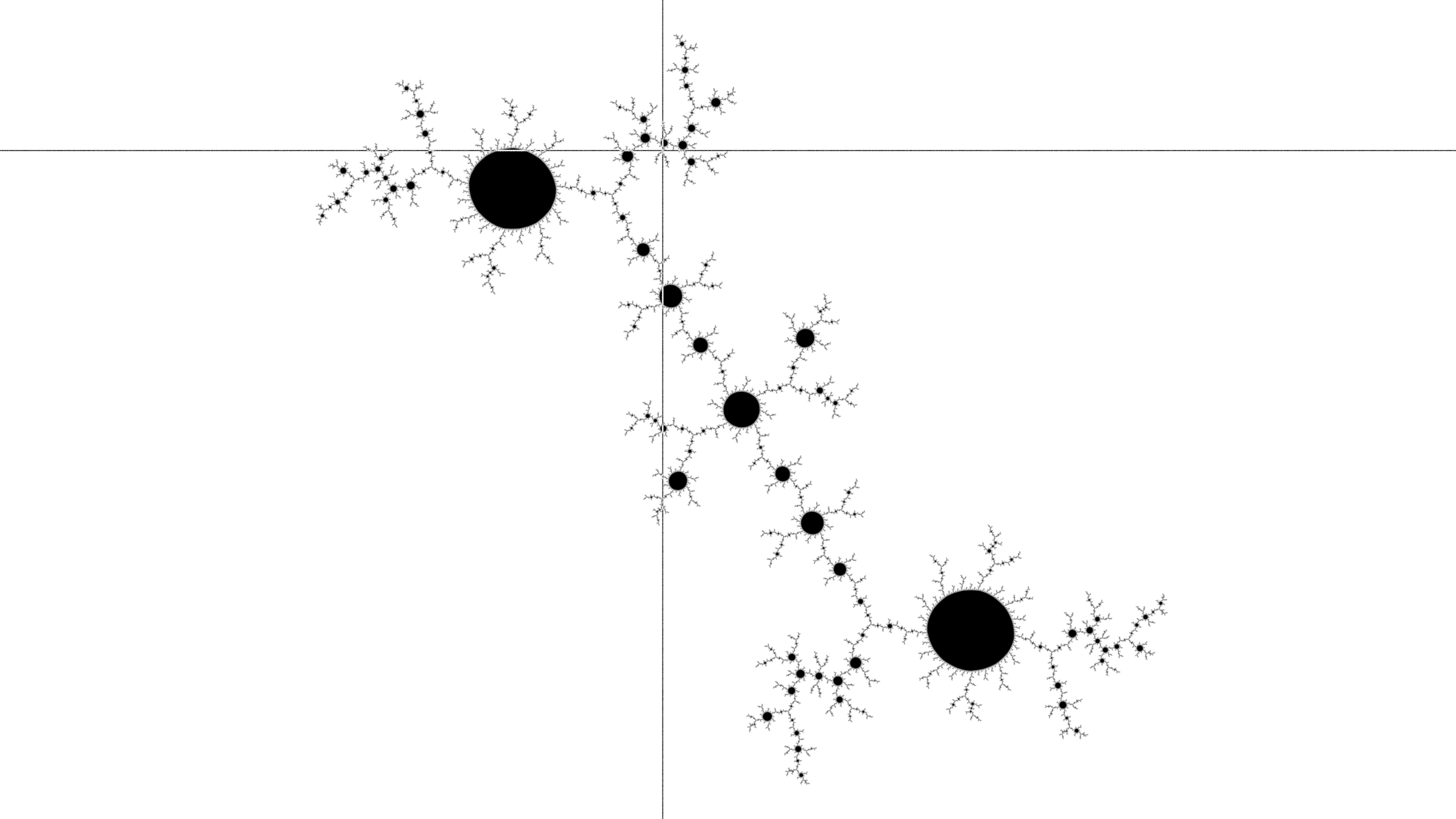
Continue to make the disk.
Continue to make the line.
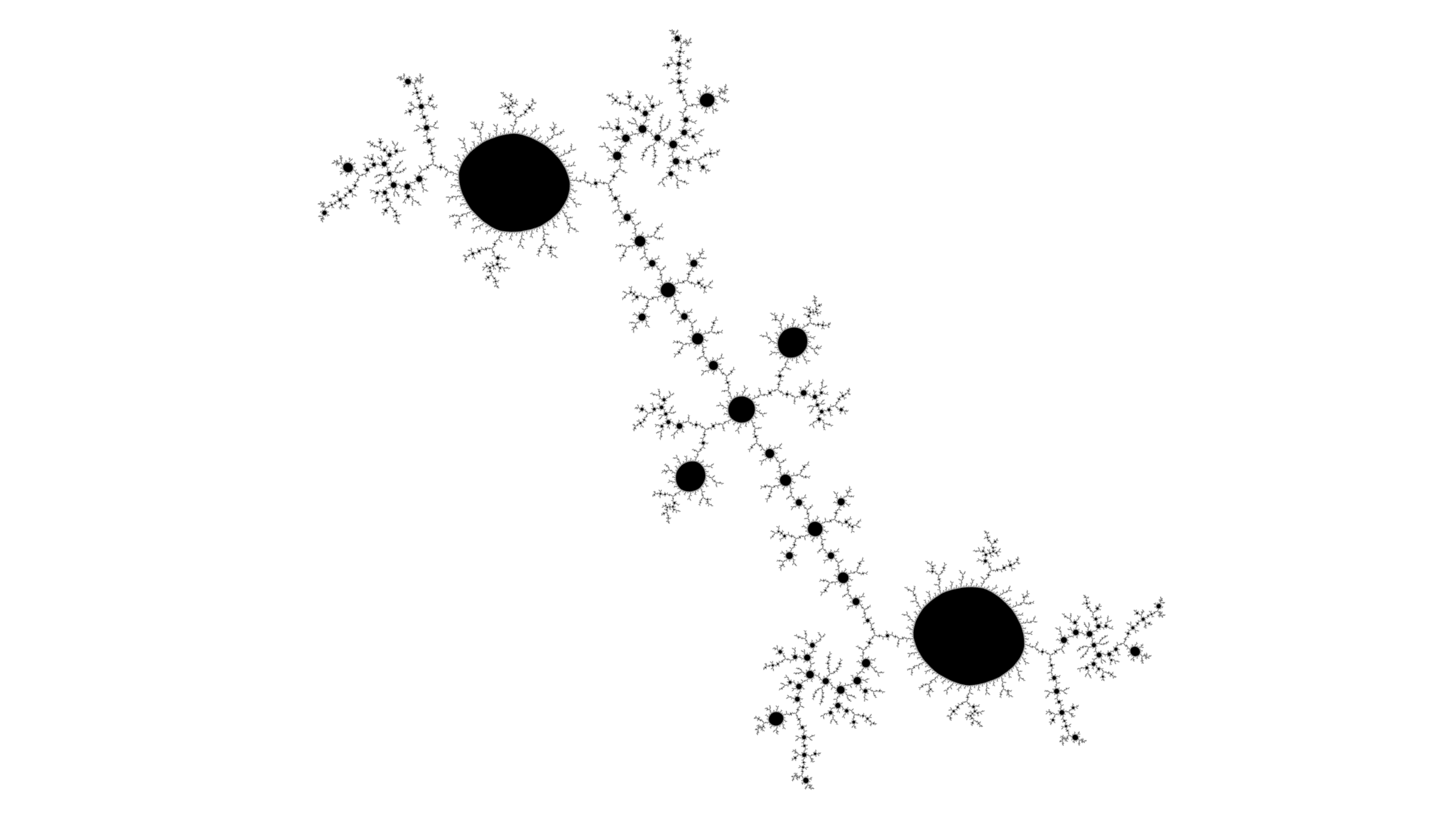
After ten mouse clicks (the initial click to choose Julia set, followed by each of the three phases developed three times), the pattern is quite satisfactory.
Continuing the process increases the refinement of the image: the main motifs contain more layers of features, and are surrounded by more layers of copies of the shapes.
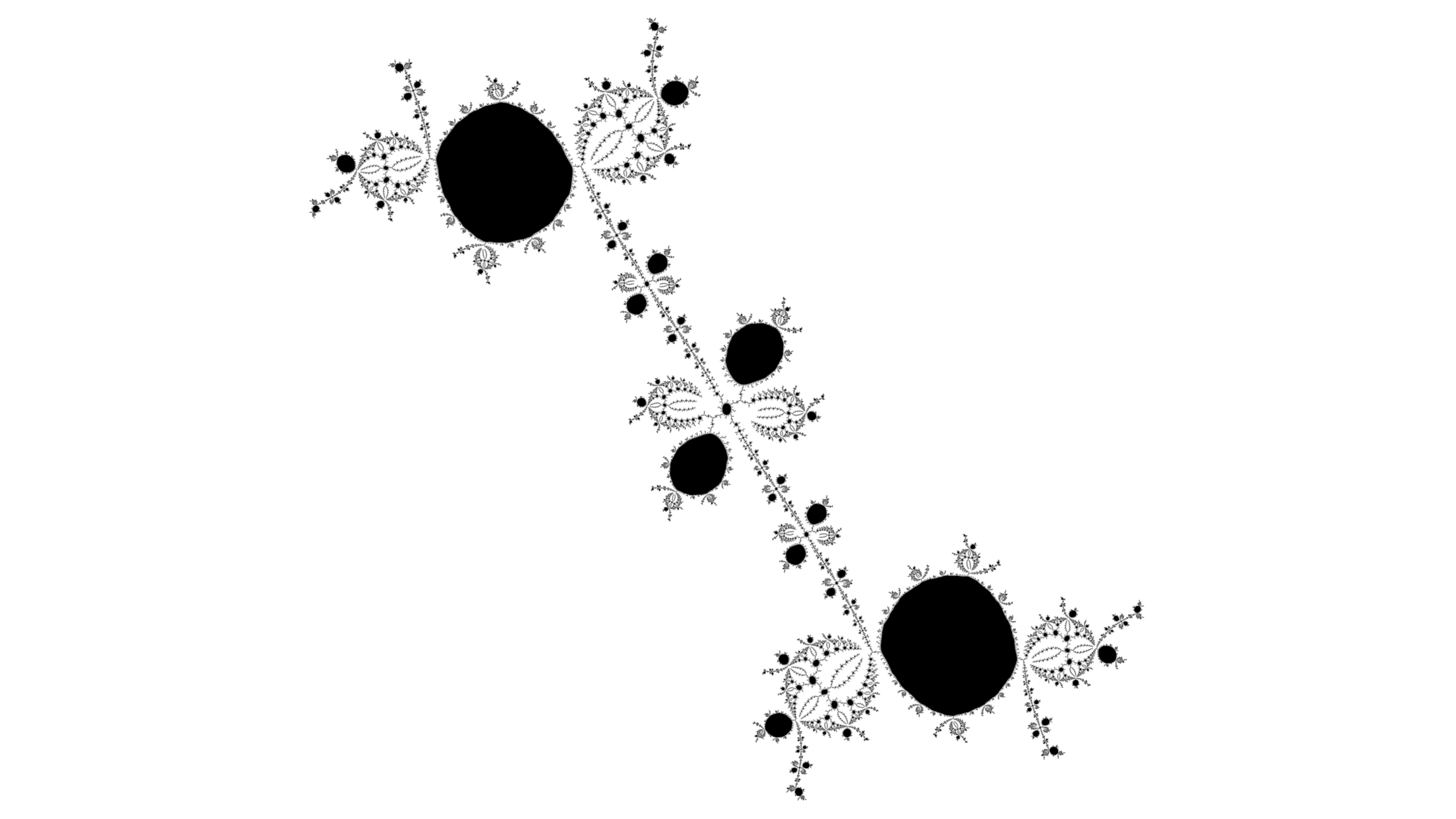
The ig link contains the parameters of the final image for the web based version of Inflector Gadget, which can be rewound and stepped through to inspect the construction process.
As discussed in my 2023 paper Patterns in Deep Mandelbrot Zooms18, points on the boundary of the Mandelbrot set are associated with (pre)periodic binary strings, namely expansions of the external angles (measured in turns) of external rays (curves from a circle at infinity that approach the Mandelbrot set along field lines). When Julia morphing in the Mandelbrot set, the length of the binary expansion goes up exponentially (for example, doubling each time).
External rays can also be defined for Julia sets, including the inflected Julia sets created by Inflector Gadget. The nodes in the Julia set have pre-periodic external angles, and when morphing the length of the binary expansions goes up linearly (for example, adding a constant number of digits each time).
In the tables, the pre-periodic part starts with . the
periodic part is surround in ( parentheses ),
and spaces are added to clarify the structure of the expansion (but they
are not significant). The expansions occur in pairs, with one ray on
either side of the filament connecting to the root of the component.
The “Iterations” column shows how many steps are taken to arrive in a neighbourhood of zero. Inflector Gadget has a quantisation feature that can snap inflection points to the exact center of nodes, which means they arrive exactly at zero. The feature was enabled for the following examples. Keeping it disabled gives a humanized softness to the otherwise somewhat cold mathematical structures.
The examples have initial point in the same baby Mandelbrot set, with
angled internal address 1 1/2 2 1/3 5 and external angle
pair [.(01011), .(01100)]. Similar patterns occur for other initial
points in the 1 1/2 2 ... wake, with the blocks of digits
replaced by the blocks of digits for the new initial point.
The “ig link” URLs contain parameters for the web-based version of Inflector Gadget, which can be rewound and stepped through to inspect the construction process.
Disk constructed by clicking in the central node.

| External Angles | Iterations | Shape |
|---|---|---|
| .(01011) .(01100) |
5 | initial |
| .0 (01011) .1 (01100) |
5 | disk |
| .00 (01011) .11 (01100) |
6 | disk |
| .000 (01011) .111 (01100) |
7 | disk |
| .0000 (01011) .1111 (01100) |
8 | disk |
| .00000 (01011) .11111 (01100) |
9 | disk |
| … | … | … |
Table 4.1: disk.
Line constructed by clicking in the main node beyond the left of the line of nodes.

| External Angles | Iterations | Shape |
|---|---|---|
| .(01011) .(01100) |
5 | initial |
| .01 0 (01011) .10 1 (01100) |
4 | line |
| .011 0 (01011) .100 1 (01100) |
3 | line |
| .0111 0 (01011) .1000 1 (01100) |
4 | line |
| .01111 0 (01011) .10000 1 (01100) |
5 | line |
| .011111 0 (01011) .100000 1 (01100) |
6 | line |
| … | … | … |
Table 4.2: line.
Tree constructed by clicking in the main node to the right of the central node.
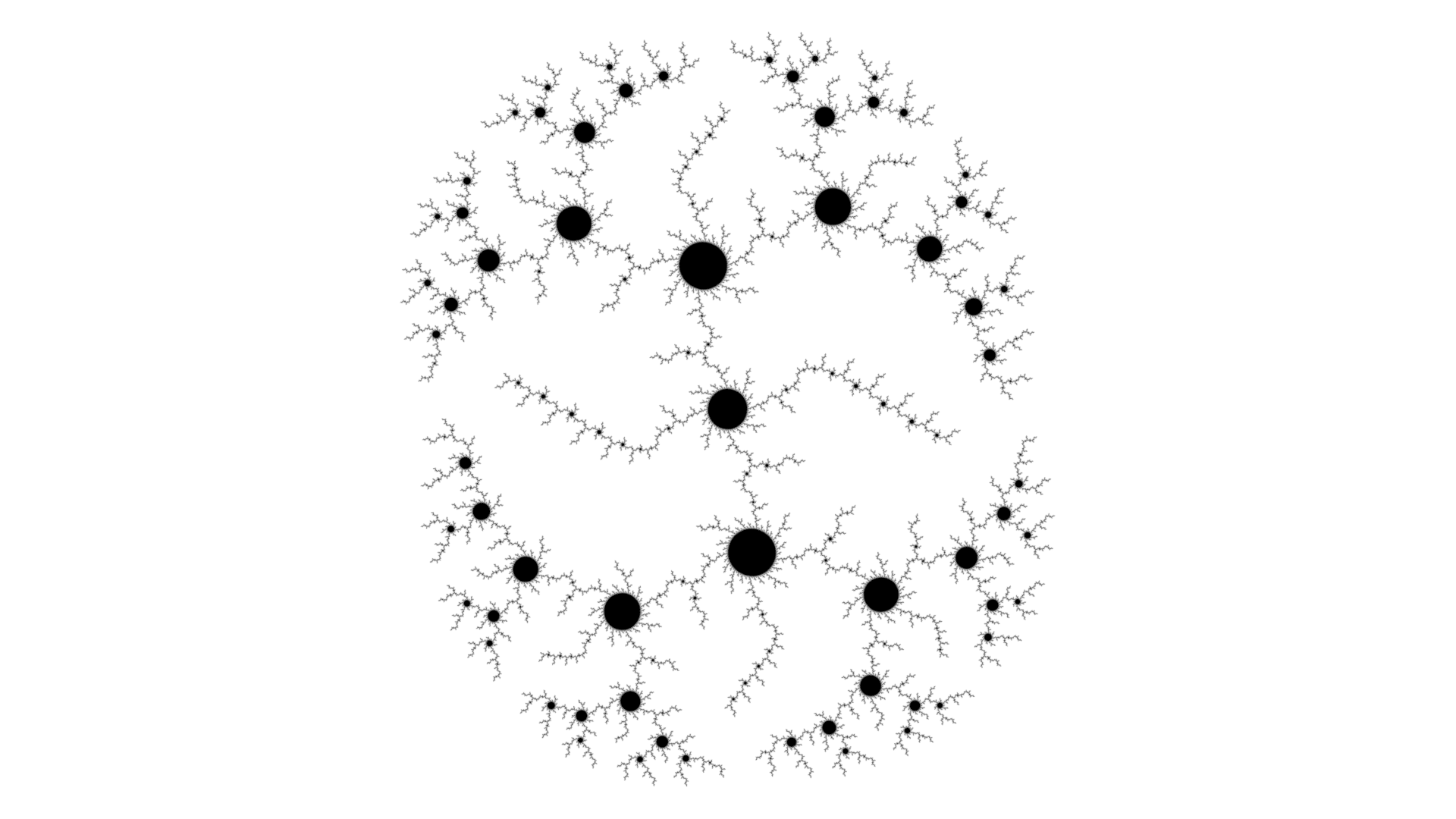
| External Angles | Iterations | Shape |
|---|---|---|
| .(01011) .(01100) |
5 | initial |
| .0 01011 10 (01011) .0 01100 01 (01100) |
7 | tree |
| .00 01011 10 10 (01011) .00 01100 01 01 (01100) |
10 | tree |
| .000 01011 10 10 10 (01011) .000 01100 01 01 01 (01100) |
13 | tree |
| .0000 01011 10 10 10 10 (01011) .0000 01100 01 01 01 01 (01100) |
16 | tree |
| .00000 01011 10 10 10 10 10 (01011) .00000 01100 01 01 01 01 01 (01100) |
19 | tree |
| … | … | … |
Table 4.3: tree.
Evolving a shape makes copies of the shape in various stages of construction, with the less-complete versions shifting outwards and shrinking at each step. The name “evolution” was coined by DinkydauSet19.
Disk evolved by clicking in the main node of the left half of the image.
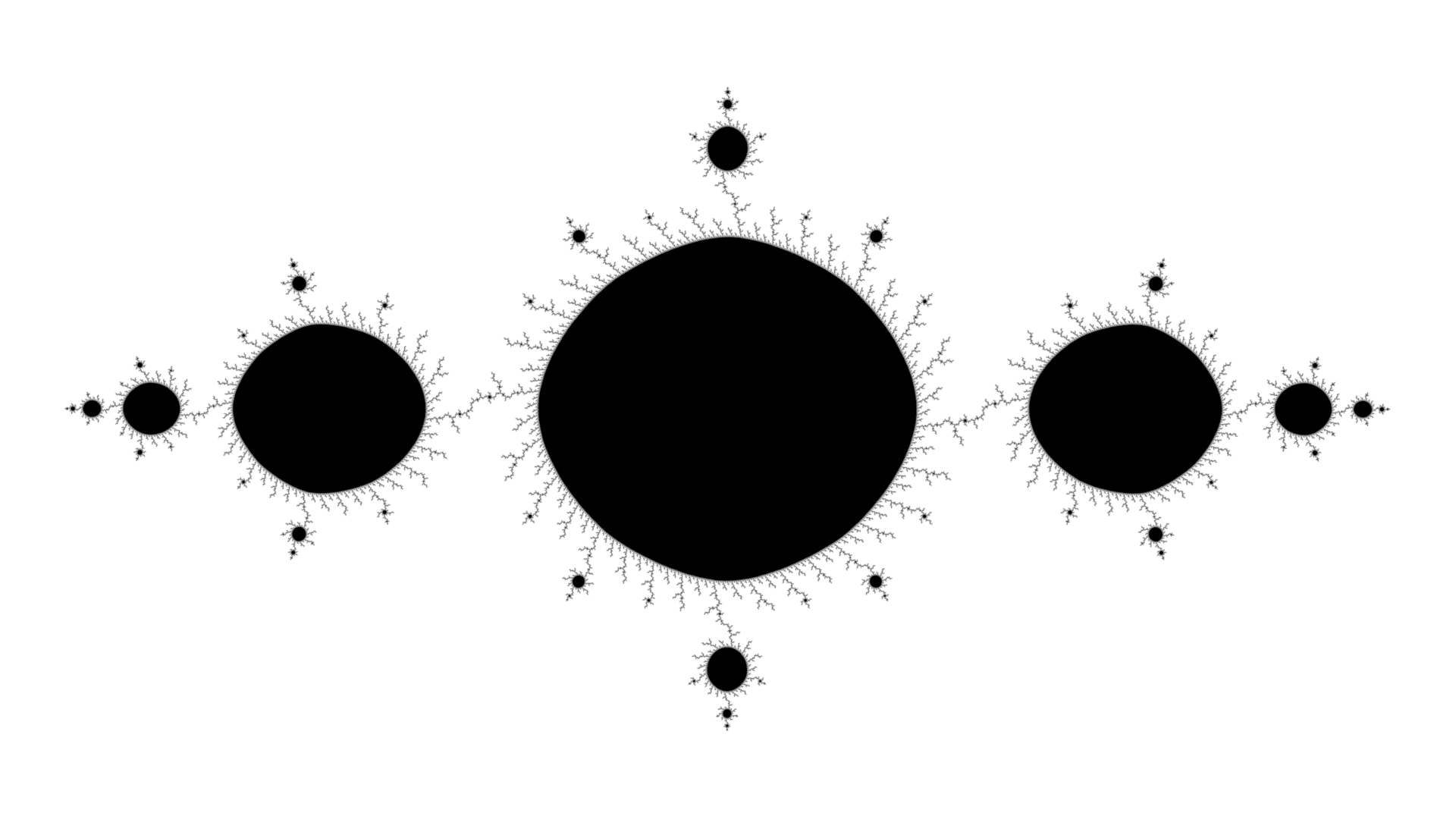
| External Angles | Iterations | Shape |
|---|---|---|
| .(01011) .(01100) |
5 | initial |
| .01 (01011) .10 (01100) |
1 | disk |
| .01 (01011) .10 (01100) |
6 | disk |
| .01 01 (01011) .10 10 (01100) |
3 | disk |
| .01 01 (01011) .10 10 (01100) |
8 | disk |
| .01 01 01 (01011) .10 10 10 (01100) |
5 | disk |
| .01 01 01 (01011) .10 10 10 (01100) |
10 | disk |
| .01 01 01 01 (01011) .10 10 10 10 (01100) |
7 | disk |
| .01 01 01 01 (01011) .10 10 10 10 (01100) |
12 | disk |
| … | … | … |
Table 4.4: evolution of disks.
Tree evolved by clicking to the right of the main node of the left half of the image.
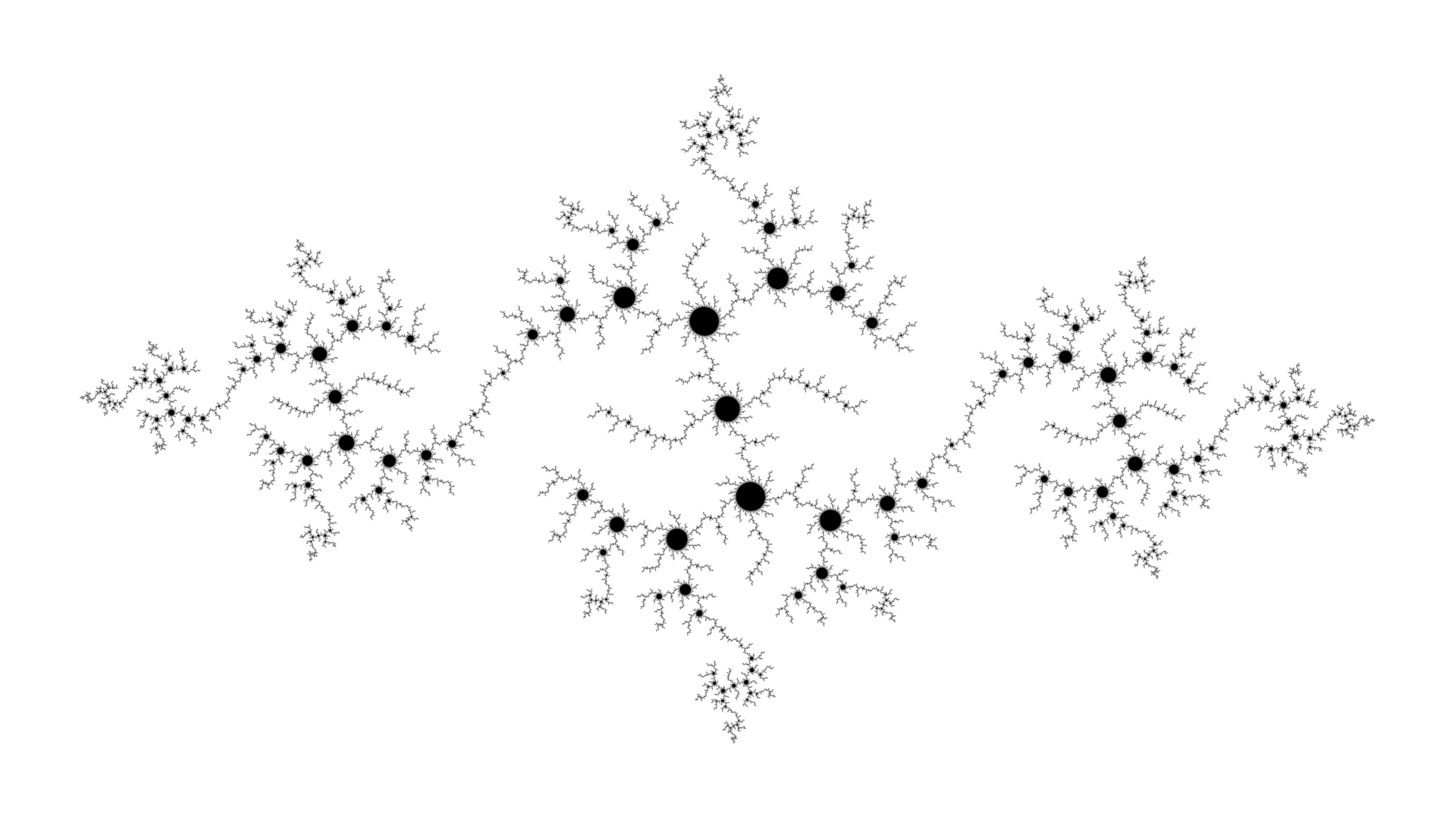
| External Angles | Iterations | Shape |
|---|---|---|
| .(01011) .(01100) |
5 | initial |
| .01 01011 10 (01011) .01 01100 01 (01100) |
8 | tree |
| .01 01011 10 (01011) .01 01100 01 (01100) |
8 | tree |
| .01 01 01011 10 10 (01011) .01 01 01100 01 01 (01100) |
12 | tree |
| .01 01 01011 10 10 (01011) .01 01 01100 01 01 (01100) |
12 | tree |
| .01 01 01 01011 10 10 10 (01011) .01 01 01 01100 01 01 01 (01100) |
16 | tree |
| .01 01 01 01011 10 10 10 (01011) .01 01 01 01100 01 01 01 (01100) |
16 | tree |
| .01 01 01 01 01011 10 10 10 10 (01011)
.01 01 01 01 01100 01 01 01 01 (01100) |
20 | tree |
| .01 01 01 01 01011 10 10 10 10 (01011)
.01 01 01 01 01100 01 01 01 01 (01100) |
20 | tree |
| … | … | … |
Table 4.5: evolution of trees.
DinkydauSet discovered parallel evolution by accident, extending the evolution method:
… there are simply two rows of shapes which can be manipulated separately! … Even better: this can be extended to more than just two. – DinkydauSet, 201420.
This is the “morph in shortest arm” strategy described above.

| External Angles | Iterations | Shape |
|---|---|---|
| .(01011) .(01100) |
5 | initial |
| .01 01011 10 (01011) .01 01100 01 (01100) |
8 | tree |
| .01 (01011) .10 (01100) |
6 | disk |
| .01 01 01011 10 10 (01011) .01 01 01100 01 01 (01100) |
12 | tree |
| .01 01 (01011) .10 10 (01100) |
8 | disk |
| .01 01 01 01011 10 10 10 (01011) .01 01 01 01100 01 01 01 (01100) |
16 | tree |
| .01 01 01 (01011) .10 10 10 (01100) |
10 | disk |
| .01 01 01 01 01011 10 10 10 10 (01011)
.01 01 01 01 01100 01 01 01 01 (01100) |
20 | tree |
| .01 01 01 01 (01011) .10 10 10 10 (01100) |
12 | disk |
| … | … | … |
Table 4.6: parallel evolution of trees and disks.
Notice how alternating trees and disks in Table 4.6 alternates between the rows of Tables 4.4and 4.5. Whether this is a coincidence or will always happen needs more research.
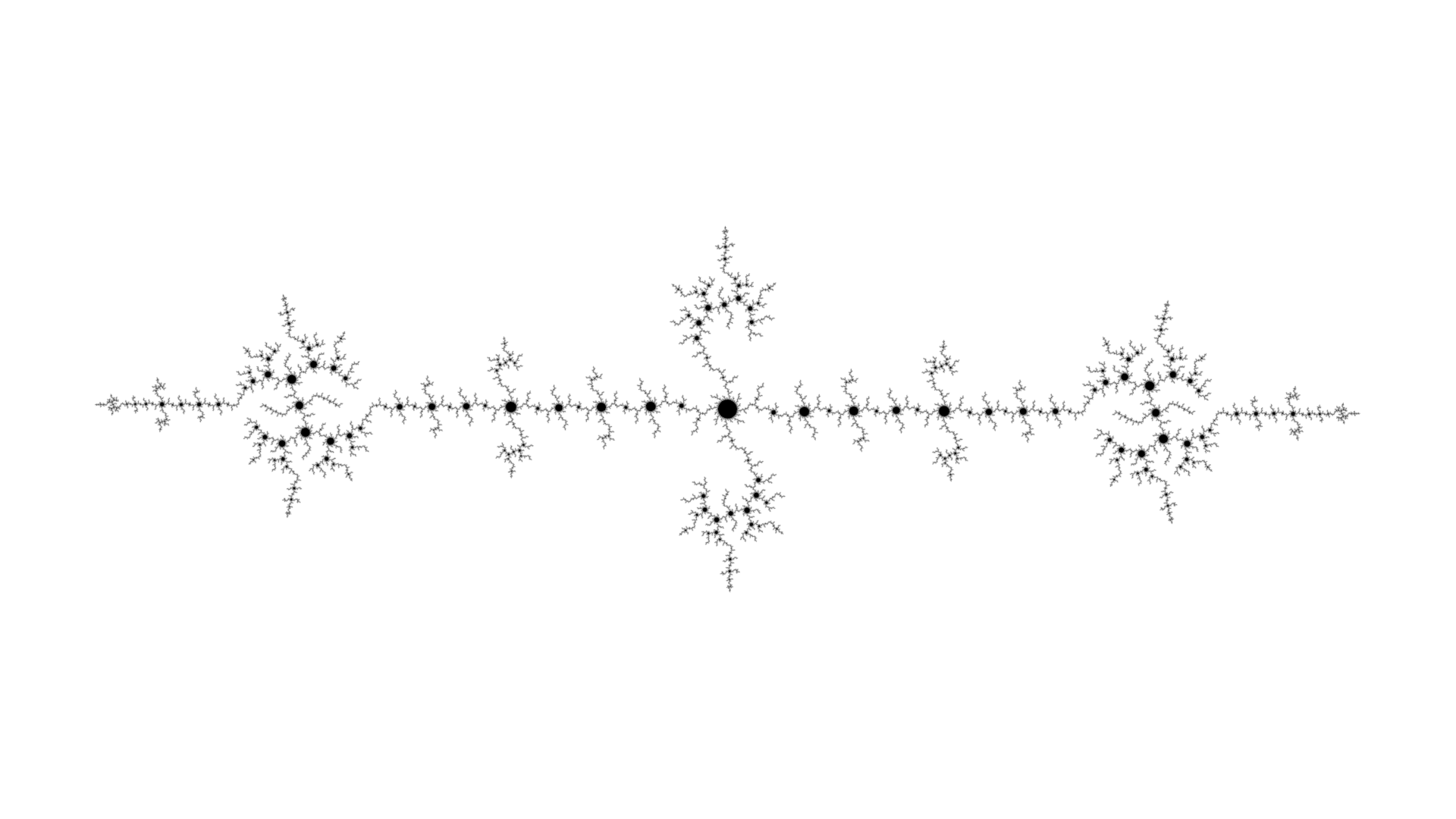
| External Angles | Iterations | Shape |
|---|---|---|
| .(01011) .(01100) |
5 | initial |
| .01 01011 10 (01011) .01 01100 01 (01100) |
8 | tree |
| .01 10 (01011) .10 01 (01100) |
3 | line |
| .01 01 01011 10 10 (01011) .01 01 01100 01 01 (01100) |
12 | tree |
| .01 10 10 (01011) .10 01 01 (01100) |
5 | line |
| .01 01 01 01011 10 10 10 (01011) .01 01 01 01100 01 01 01 (01100) |
16 | tree |
| .01 10 10 10 (01011) .10 01 01 01 (01100) |
7 | line |
| .01 01 01 01 01011 10 10 10 10 (01011)
.01 01 01 01 01100 01 01 01 01 (01100) |
20 | tree |
| .01 10 10 10 10 (01011) .10 01 01 01 01 (01100) |
9 | line |
| … | … | … |
Table 4.7: parallel evolution of trees and lines.
To evolve three shapes in parallel, the initial point should be in
the wake of a period 3 component of the Mandelbrot set. There are three
of these: the largest disks at the top and bottom of the cardioid (whose
Julia sets are colloquially called “rabbits”), and the largest baby
Mandelbrot set in the antenna on the left (whose Julia set is
colloquially called the “airplane”). This example uses a period 4 baby
Mandelbrot set with angled internal address 1 1/3 3 1/2 4
and external angle pair [.(0011), .(0100)].
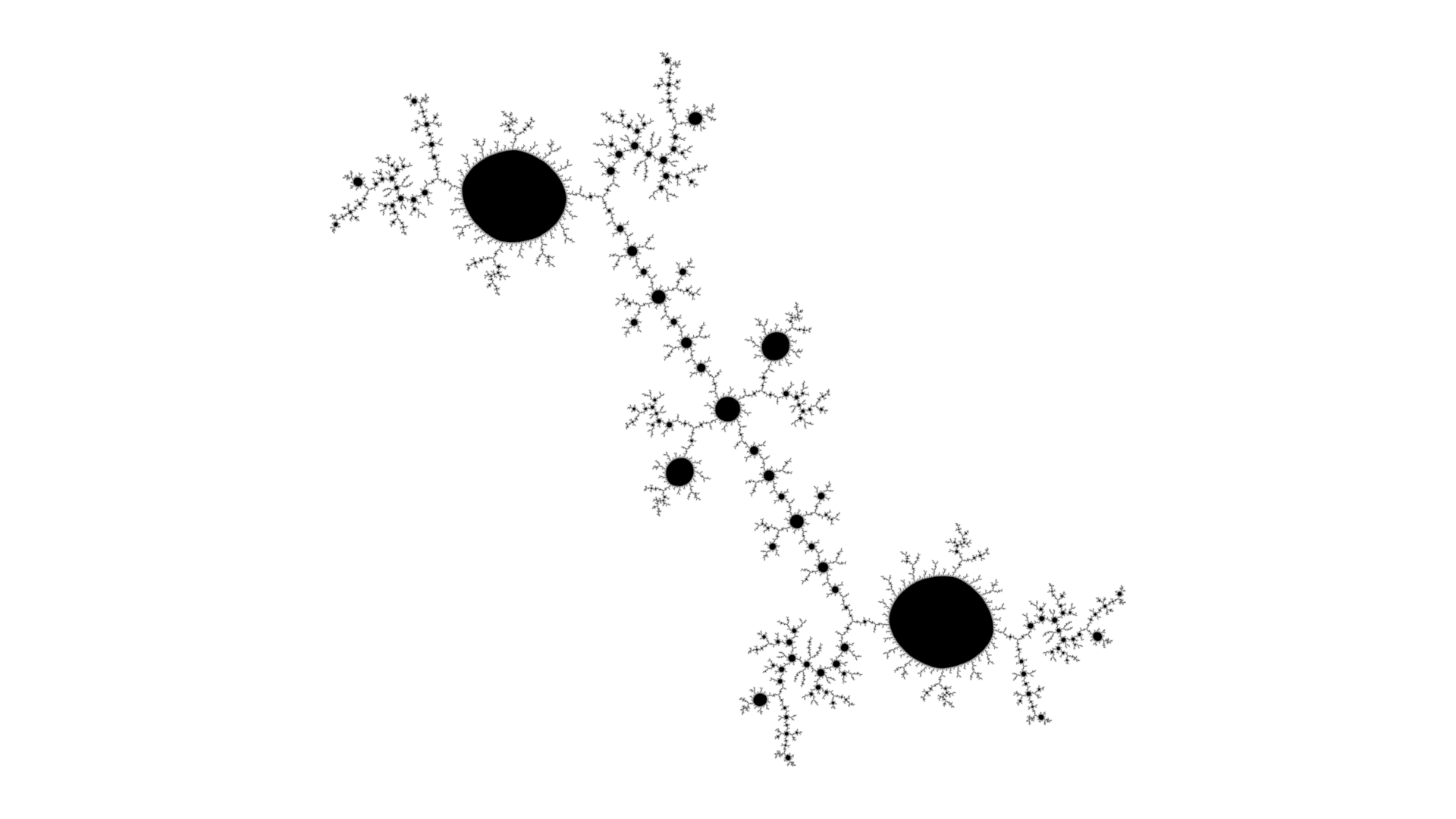
| External Angles | Iterations | Shape |
|---|---|---|
| .(0011) .(0100) |
4 | initial |
| .001 0011 010 (0011) .001 0100 001 (0100) |
9 | tree |
| .001 (0011) .010 (0100) |
2 | disk |
| .001 010 (0011) .010 001 (0100) |
5 | line |
| .001 001 0011 010 010 (0011) .001 001 0100 001 001 (0100) |
15 | tree |
| .001 001 (0011) .010 010 (0100) |
5 | disk |
| .001 010 010 (0011) .010 001 001 (0100) |
8 | line |
| .001 001 001 0011 010 010 010 (0011) .001 001 001 0100 001 001 001 (0100) |
21 | tree |
| .001 001 001 (0011) .010 010 010 (0100) |
8 | disk |
| .001 010 010 010 (0011) .010 001 001 001 (0100) |
11 | line |
| … | … | … |
Table 4.8: 3rd order evolution of trees, disks and lines (rabbit).
… the shape of which the evolution is shown, can be an evolution set itself … – DinkydauSet, 201521.
Evolution of trees constructed as above, within the focused arm, interleaved with simple disks.

| External Angles | Iterations | Shape |
|---|---|---|
| .(01011) .(01100) |
5 | initial |
| .01 01100 10 01011 01 (01011) .10 01011 01 01100 10 (01100) |
15 | trees |
| .01 (01011) .10 (01100) |
6 | disk |
| .01 10 01011 01011 01 (01011) .10 01 01100 01100 10 (01100) |
15 | trees |
| .01 01 (01011) .10 10 (01100) |
8 | disk |
| .01 10 01 01100 10 01011 01 01 (01011)
.10 01 10 01011 01 01100 10 10 (01100) |
21 | trees |
| .01 01 01 (01011) .10 10 10 (01100) |
10 | disk |
| .01 10 01 10 01011 01011 01 01 (01011)
.10 01 10 01 01100 01100 10 10 (01100) |
21 | trees |
| .01 01 01 01 (01011) .10 10 10 10 (01100) |
12 | disk |
| .01 10 01 10 01 01100 10 01011 01 01 01
(01011) .10 01 10 01 10 01011 01 01100 10 10 10 (01100) |
27 | trees |
| .01 01 01 01 01 (01011) .10 10 10 10 10 (01100) |
14 | disk |
| .01 10 01 10 01 10 01011 01011 01 01 01
(01011) .10 01 10 01 10 01 01100 01100 10 10 10 (01100) |
27 | trees |
| .01 01 01 01 01 01 (01011) .10 10 10 10 10 10 (01100) |
16 | disk |
| … | … | … |
Table 4.9: evolution of (evolution of trees) and disks.
The history of Inflector Gadget is short compared to the history of Mandelbrot deep zooms. The proposed strategies for designing patterns follow the natural dynamics of the system: combined with repetition of inflection point selection choices this leads to regular patterns, but “freestyle” play is also possible. The examples analysed are inspired by DinkydauSet’s deep Mandelbrot set zooms, but are created in a fraction of the time.
Inflector Gadget is a fractal design tool, contrasting with fractal exploration tools like most Mandelbrot set software. One can design shapes with an exploration tool but it’s easier with a dedicated design tool. Other genres of fractal art have incorporated design from a much earlier point in their history - fractal flames (non-linear iterated function systems) were popularized by the Electric Sheep22 distributed screen saver project in 1999, and can be designed with software such as Apophysis23, Chaotica24 and IFSRenderer25.
Future work includes extending the analysis to synthesis, algorithmically generating later external angles in each sequence and tracing their rays inwards to find the corresponding inflection points.
Achieving this in a semi-automatic way would be a matter of the artist first invoking the outwards external ray tracing feature of Inflector Gadget at each inflection point, analysing (by hand) the printed strings of binary digits into (pre-)periodic parts and inferring the structure, as the author did in the Analysis section above. The artist can then write short bespoke algorithms to generate sequences of external angles that correspond to the desired pattern, which could then be copy/pasted into a future version of Inflector Gadget.
Inflector Gadget will be extended (as the author’s time allows) to have the required numerical algorithms to construct the inflected Julia set from the symbolic description as a sequence of external angles. “Humanised” variations (rather than the rigidly quantized version that is mathematically easiest to construct) can then be constructed by stochastic means, varying the automated click position according to pseudo-randomly generated numbers.
Full automation is an open question for further research: to write an algorithm so that the artist can construct a pattern by hand with a few rounds of development, then activate a button, and the computer continues the process as far along as the artist desires.
The author thanks the anonymous reviewers for their in depth and thoughtful feedback.
Claude Heiland-Allen. 2023. “Patterns in Deep Mandelbrot Zooms.” In Algorithmic Pattern Salon. Then Try This. https://doi.org/10.21428/108765d1.7c2589c1↩︎
K.I. Martin. 2013. “SuperFractalThing Maths.” https://web.archive.org/web/20130701075021/http://superfractalthing.co.nf/sft_maths.pdf↩︎
DinkydauSet. 2013-09-25. “Evolution of Trees.” https://www.deviantart.com/dinkydauset/art/Evolution-of-trees-402876071↩︎
DinkydauSet. 2014-05-07. “Parallel Evolution.” https://www.deviantart.com/dinkydauset/art/Parallel-evolution-452515257↩︎
Chillheimer. 2016. “Kalle’s Fraktaler 2.” https://web.archive.org/web/20160318153101/http://www.chillheimer.de/kallesfraktaler/↩︎
stardust4ever. 2014. “Re: (Attn: stardust4ever) Magnum Opus Ex full zoom.” https://ff1.fractalforums.org/index.php?topic=19144.msg75848#msg75848↩︎
Kalle’s Fraktaler. 2014. “Kalles Fraktaler 2.5.9 - Show Inflection.” https://web.archive.org/web/20160414224025/http://www.fractalforums.com/kalles-fraktaler/kalles-fraktaler-2-5-9-show-inflection/ https://ff1.fractalforums.org/index.php?topic=19812.msg76343#msg76343↩︎
Fractal Universe. 10 years ago (as of April 2025). “Mandelbrot zoom in unattainable julias morphing, simulation with Ultra Fractal.” https://www.youtube.com/watch?v=pFQn2rnWX7E↩︎
DinkydauSet. 2017-01-17. “5th order Evolution of evolution (model).” https://www.deviantart.com/dinkydauset/art/5th-order-Evolution-of-evolution-model-657912155↩︎
Claude Heiland-Allen. 2025. “Inflector Gadget home page.” https://mathr.co.uk/web/inflector-gadget.html↩︎
Dinkydau. 2018. “Explore fractals (inflection tool).” https://fractalforums.org/index.php?topic=777.msg3984#msg3984↩︎
Dinkydau. 2020. “Re: Explore fractals (inflection tool).” https://fractalforums.org/index.php?topic=777.msg18680#msg18680↩︎
Claude Heiland-Allen. 2025. “Inflector Gadget web version.” https://mathr.co.uk/ig/↩︎
Isaac Hew. 2024. “Mandelbrot Simulation #1.” https://www.youtube.com/watch?v=CxArJzuKs6w↩︎
Isaac Hew. 2024-05-11. “Mandelbrot Simulation #2.” https://www.youtube.com/watch?v=huwVbdM_duc↩︎
Isaac Hew. 2024-05-20. “Mandelbrot Simulation #3.” https://www.youtube.com/watch?v=Ij6LwgtZArI↩︎
Karl Sims. No date (earliest archive.org copy 2013). “Understanding Julia and Mandelbrot Sets.” https://www.karlsims.com/julia.html (accessed 2025-04-09)↩︎
Claude Heiland-Allen. 2023. “Patterns in Deep Mandelbrot Zooms.” In Algorithmic Pattern Salon. Then Try This. https://doi.org/10.21428/108765d1.7c2589c1↩︎
DinkydauSet. 2013-09-07. “Prototype of Evolution.” https://www.deviantart.com/dinkydauset/art/Prototype-of-evolution-399217546↩︎
DinkydauSet. 2014-05-07. “Parallel Evolution.” https://www.deviantart.com/dinkydauset/art/Parallel-evolution-452515257↩︎
DinkydauSet. 2015-01-04. “Evolution of Evolution.” https://www.deviantart.com/dinkydauset/art/Evolution-of-evolution-504745684↩︎
Wikipedia. Electric Sheep. https://en.wikipedia.org/wiki/Electric_Sheep (accessed 2025-07-30)↩︎
Wikipedia. “Apophysis (software).” https://en.wikipedia.org/wiki/Apophysis_(software) (accessed 2025-07-30)↩︎
Chaotica. “Chaotica.” https://www.chaoticafractals.com/ (accessed 2025-07-30)↩︎
bezo97. “IFSRenderer.” https://github.com/bezo97/IFSRenderer (accessed 2025-07-30)↩︎