Published September 2025 as part of the proceedings of the first Alpaca conference on Algorithmic Patterns in the Creative Arts, according to the Creative Commons Attribution license. Copyright remains with the authors.
doi:10.5281/zenodo.17084422
Across cultures and centuries, pattern-making has served as a way to translate systems of belief, ritual, and social order into visual form. Traditions such as Aztec sunstone carvings, Celtic knots, and South Indian Kolams reflect distinct ways of encoding meaning through repetition, symmetry, and spatial reasoning. Creative coding offers a way to engage with these systems beyond external subjects of analysis, but as generative collaborators, opening pathways to build tools that extend their logic into new, expressive forms.
Among these traditions, Pulli Kolams, looped line drawings built on dot grids from South India offer a uniquely generative starting point. Celebrated for the several mathematical concepts they relate to, Kolams are approached as active collaborators in code. They serve as both structure and an invitation:
How might we design systems that are both computationally generative and culturally grounded, open to experimentation while honoring the collective knowledge they emerge from?
Two process methods guide this inquiry:
Recursive construction: Using Turtle graphics in Python, Kolams are generated as continuous looping lines, following a similar procedural logic when drawing them by hand. This method parallels Islamic interlace patterns, macramé knotting techniques, and Celtic knotwork—traditions where patterns emerge through rule-based traversal and interconnection. These recursive drawings reflect not only visual complexity but also processes of memory, repetition, and continuity.
Tiling systems: This JavaScript-based approach starts with the visual form of a Kolam and deconstructs it into modular tile units defined by curvature and grid permutations, constrained by aesthetic logic. The resulting pattern language supports motif-style tiling that preserves visual continuity, drawing on the Tatreef motifs, Kente weaving structures, and principles akin to Truchet tiling.
Traditions like Islamic interlace design, macramé knotting, Kente and Mayan weaving, Filipino Binituwon, Māori textiles, Kolams and several others embody sophisticated mathematical principles—symmetry, recursion, spatial logic—and often predate the formal discoveries we use to analyze and explain them. These traditions don’t illustrate science, they are science. They represent rigorous knowledge systems developed through observation, repetition, and ritual. Studying them in their own right opens the door to deeper, more expansive forms of understanding.
This work centers Kolams as one such system and explores the possibility of an evolving, shared language of pattern-making. It uses open-source tools and code based platforms to honor, extend, and connect these traditions. It frames pattern-making as a site of cross-cultural dialogue, where computation is not just a means of representation, but a bridge between meaning systems.
As we consider the idea of a universal pattern language, it becomes essential to ask: what constitutes a pattern? Patterns are not just visual decoration. Across cultures, they are systems of meaning—expressing ritual, repetition, and relationship. Visual systems like Pulli Kolams, Islamic interlace, Kente cloth, and Tatreez embroidery share structural principles that can be translated into algorithms.
Contemporary industrial environments are increasingly characterized by a lack of ornamentation, symbolic meaning, and cultural specificity—features once integral to the expression of identity and craftsmanship. At the same time, advancements in technology and global connectivity have expanded our capacity to engage with diverse knowledge systems across cultures and disciplines. This intersection offers a critical opportunity to reintroduce complexity, intentionality, and cultural context into our designed environments through collaborative and informed modes of creation.
Through technology and code, we’ve explored their geometric and mathematical logic. Using tools like recursive logic or tiling systems, we can represent and remix these forms in ways we can represent and remix these forms in ways that stay rooted in their origins while opening space for new interpretations.The question is not just how to study patterns and use code to deconstruct their logic, but how to co-create them. Can we use code to recognize shared logics and design tools that support pattern exchange across cultures? This gives us the opportunity to reimagine pattern-making—not as static tradition, but as collaborative and evolving design.
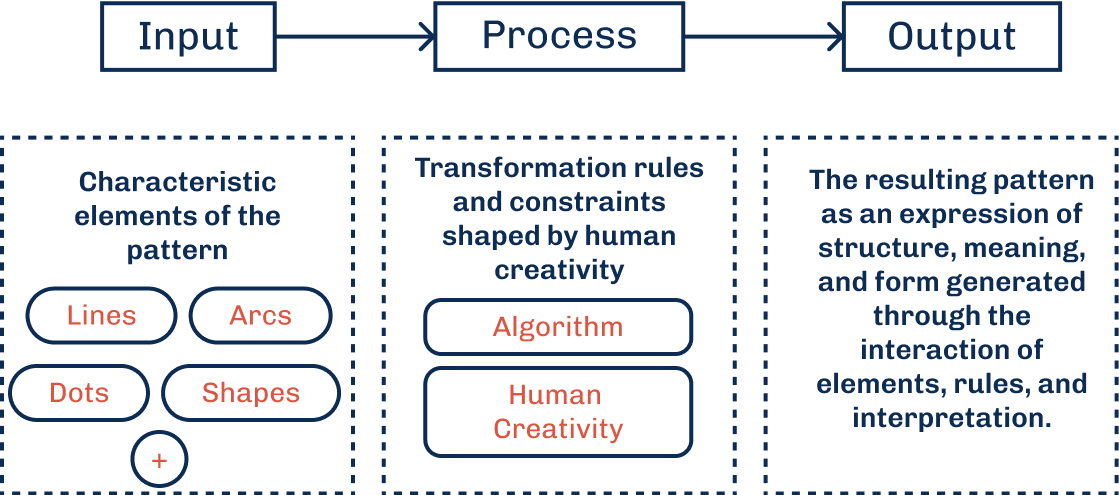
A generalized system for understanding pattern-making can be framed through an Input–Process–Output (IPO) model. This framework aligns with traditional and cultural practices, where the input comprises raw materials such as fabric, rice flour, or tools. The process is driven by human creativity and labor, operating within a set of rules, constraints, and transformations that result in the output: a completed pattern.
When adapted to computational contexts, the emphasis often shifts toward the algorithmic dimension. Inputs are translated into visual elements structured for algorithmic interpretation and manipulation. Despite the use of technology, this approach aims to maintain the central role of the human collaborator,the creator as an active agent in the generative system, rather than positioning the algorithm as a replacement.
The basic components that form a pattern: dots, lines, shapes, and other visual elements.
The process involves two intertwined parts:
The resulting pattern: a co-created, evolving visual form shaped by both system logic and human interpretation.

This study examines two distinct input-process methods for generating Kolams and identifies shared logics and pattern elements that can be applied across similar generative processes.
There are a set of rules that follow what is specifically identified as a pulli kolam. They are as follows:
Rules for Drawing a Kolam
Dot Grid Foundation: Kolams begin with a grid of dots (pullis), which serve as guides. Lines are drawn around these dots without touching them directly.
Symmetry: Traditional kolams often follow symmetry — along the x-axis, y-axis, or display radial symmetry from the center.
Line Intersections: Lines may intersect, but typically only once at a given point. Excessive overlapping is avoided.
Angle and Orientation: Lines are often drawn at 45° inclines, especially when using square or diamond-shaped grids, as in this implementation.
In this approach, the physical act of drawing a Kolam serves as the foundation for its construction. Dots are arranged within a grid-like structure, forming the underlying framework.The Kolam emerges through a continuous sequence of loops, which include arcs and straight lines, and follow traditional patterns and principles of symmetry. The grid size can be adjusted to match the desired scale of the Kolam.
For the purpose of this demonstration, We will look at 4-fold radial symmetry and assume only one continuous line drawing(or loop) that encircles the dots. Technically, multiple continuous loops following different paths can be combined to complete a Kolam. We will review this briefly towards the end.
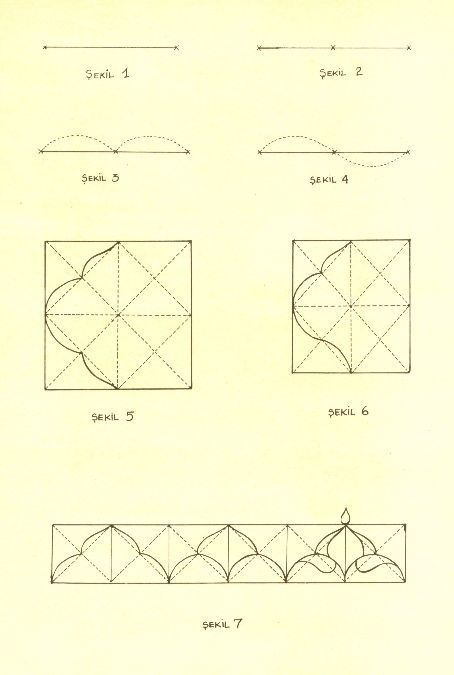
The composition starts with a straight line drawn from the center at a 45 degree angle across the dotted grid and the looping is extended around the other pullis(dots)laid out as a foundation. Drawing straight lines diagonally between the dots is what connects the other path types of the kolam that loops around the remaining dots. This same path is repeated along each of the 4 axes. This straight line is the the most basic path type that serves to connect or provide direction between the other path types and shift the loop across rows or columns, depending on its direction. We will call this path type 0.
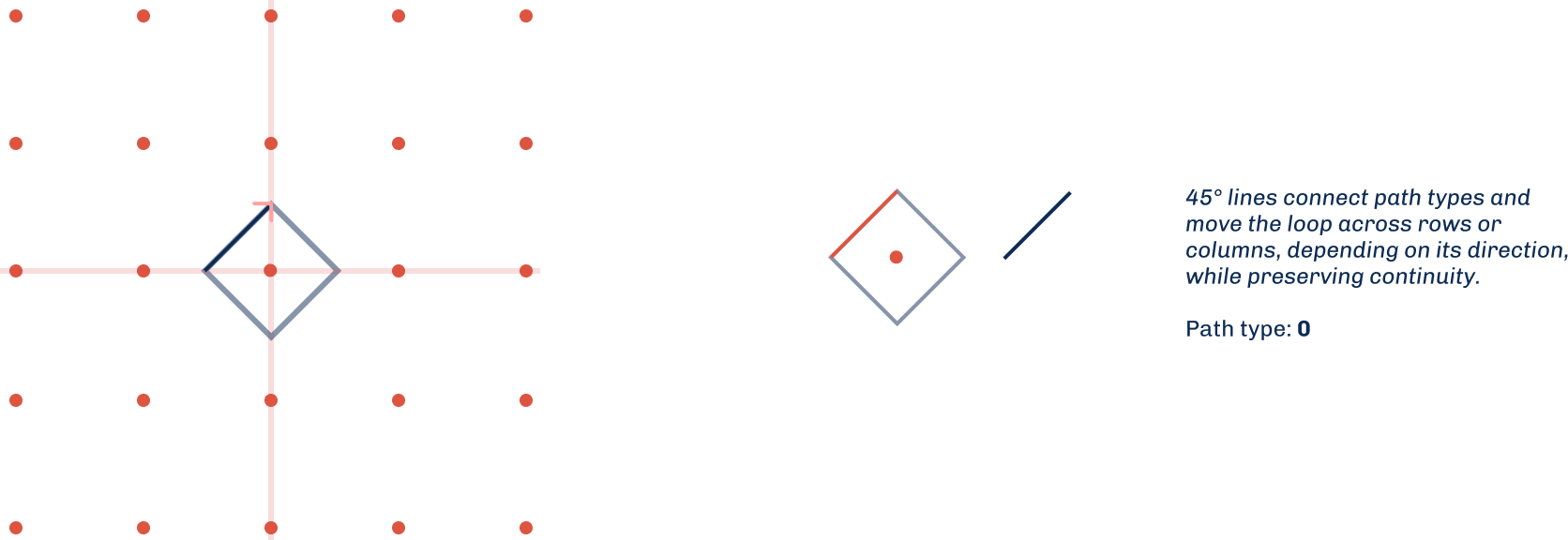
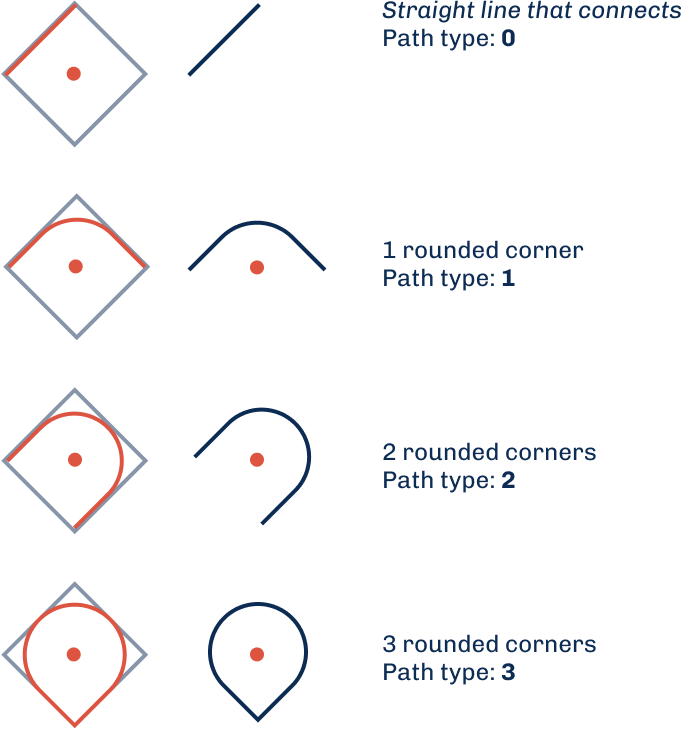
A single-line Kolam drawing is composed of four fundamental path types, three of which are actively used in construction. These will be our inputs, each characterized by the number of rounded corners of a square’s vertices. These path types feature one, two, or three rounded corners respectively, as shown in Figure 2. Each rounded corner maintains a radius equal to half the square’s side length, creating consistent geometric proportions. By assigning numerical values to these path types, the drawing process can be systematized through algorithmic looping functions.
The traversal across the grid follows a defined set of rules that shape the unique form of a Kolam. Figures 3 and 4 illustrate these rules. showing two case scenarios: 1. Within a single row or column of the grid, the path moves around the dots (pullis) following different path types: from Path type 1 to Path type 2 [1,2], from Path type 1 to itself [1,1], or from Path type 2 to Path type 3[2,3]. Path type 3 forms a closed loop that typically marks the end of a Kolam. These path movements are denoted by numerical pairs in brackets.
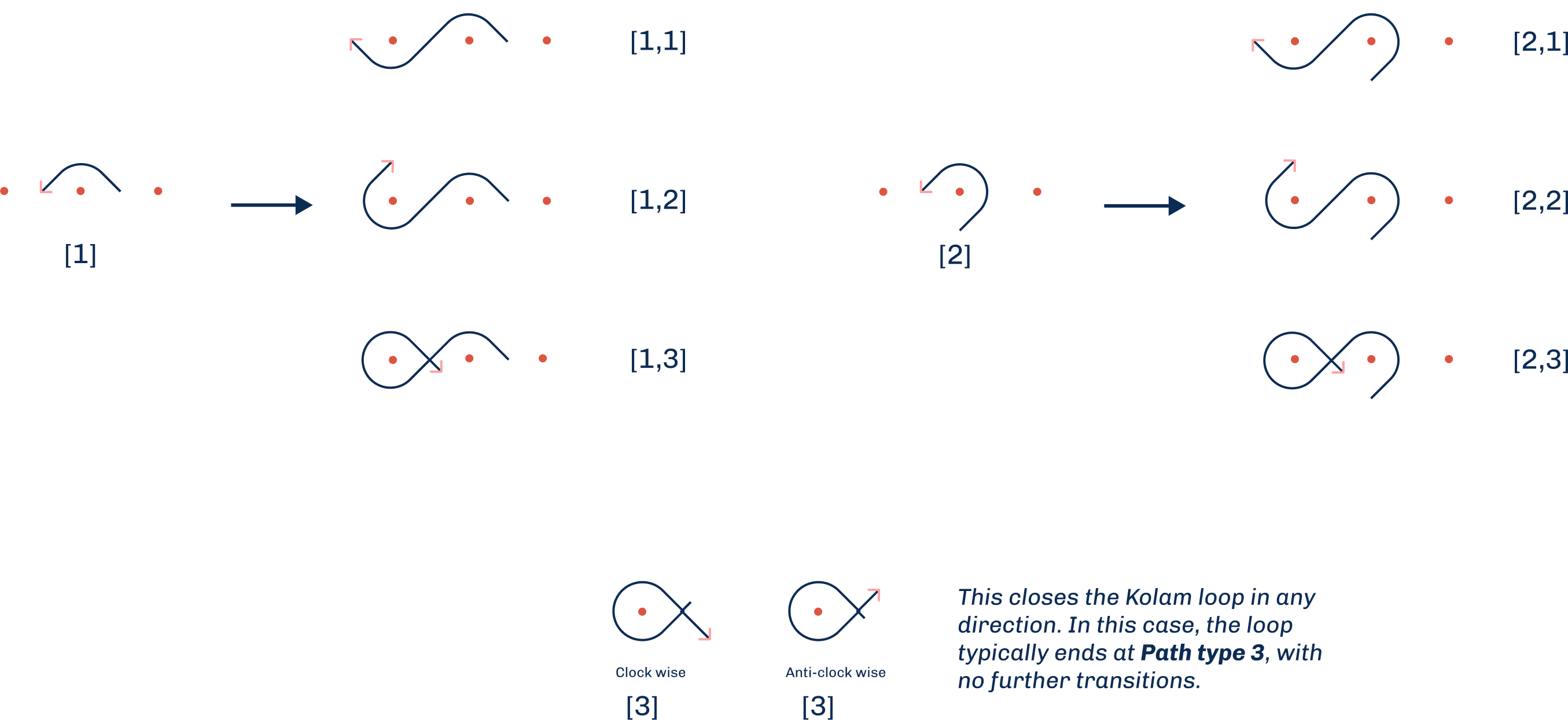
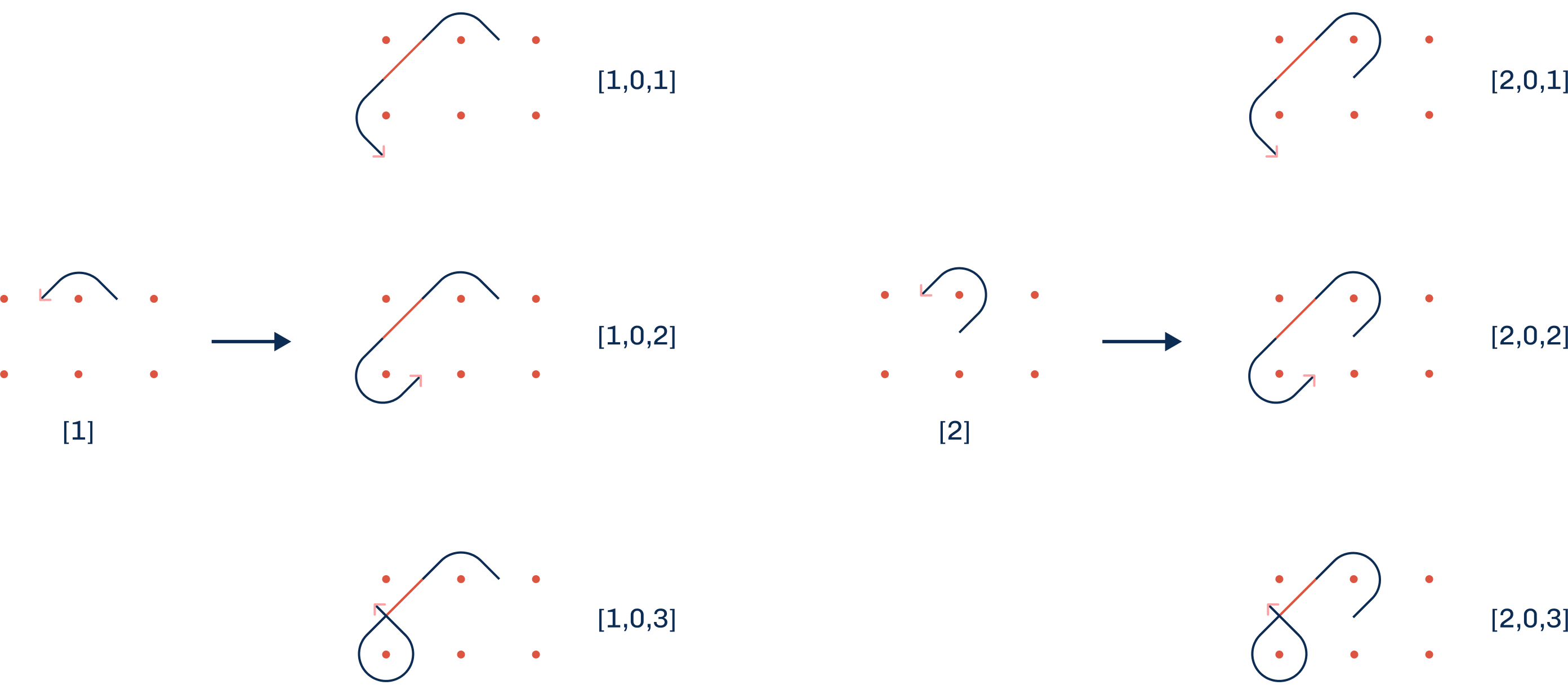
The completion of a Kolam is determined by the specific sequence of path types traversed across the grid of pullis (dots). The loop is finalized by closing the path to form a continuous geometric figure—resulting in a finished Kolam. If, during traversal, the path intersects itself or returns to its starting point before all pullis are encircled, additional Kolam loops may be required. In such cases, subsequent loops must account for the pullis that haven’t been encircled, constrained by the spatial configuration of the already-closed segments. This represents a more advanced scenario involving multiple Kolam loops.
In the scenario under consideration, loop closure is initiated upon encountering Path type 3. From this point, the path reverses the sequence of prior transitions to complete the loop. For the purposes of this demonstration, we assume the path remains within its originating quadrant and that closure begins immediately after Path type 3. The Kolam is thus completed using a single continuous line that encircles all relevant pullis.
The loop closure follows these guiding principles: 1. Path type 1 closes with Path type 1 2. Path type 2 closes with Path type 0 3. Path type 0 closes with Path type 2
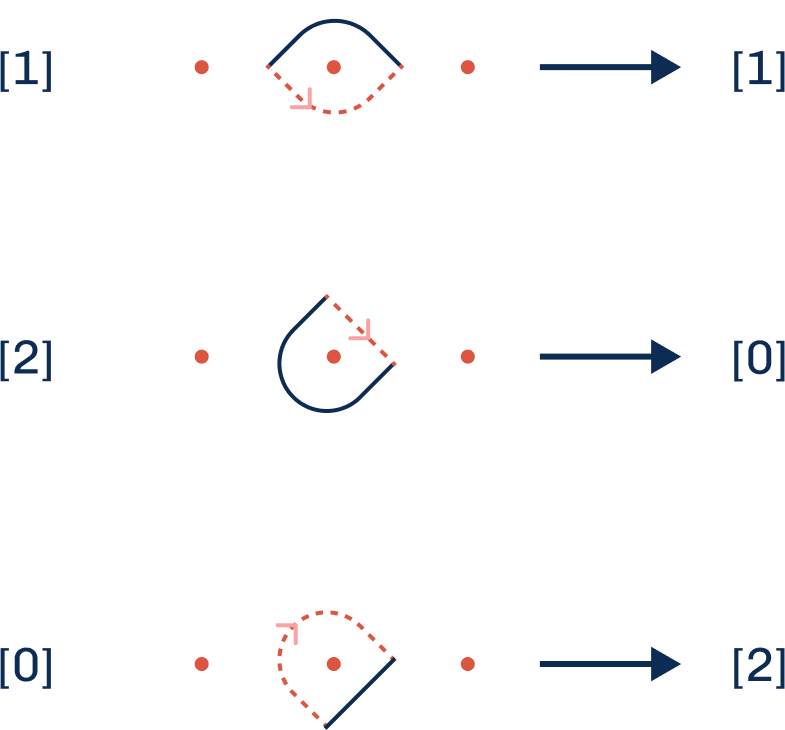
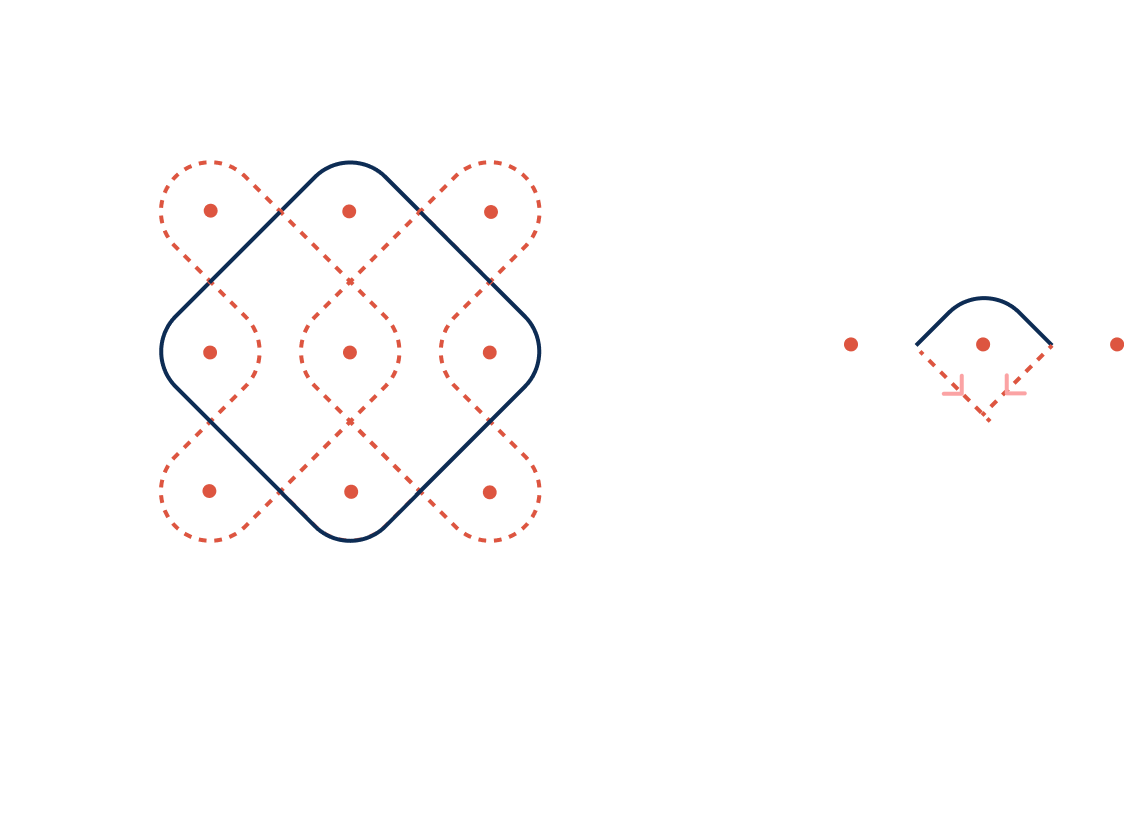
Figure 7 presents the fundamental Kolam structure, denoted as Kolam[3], which consists of Path type 3 repeated in each quadrant. By convention, the loop begins in the upper-left quadrant of the grid which corresponds to the second quadrant in Cartesian terms.
![Figure 7: Steps demonstration the creation process of Kolam[3]](media/f5e70194ea22b67c3e18b3b16e2ad212217f0862.png)
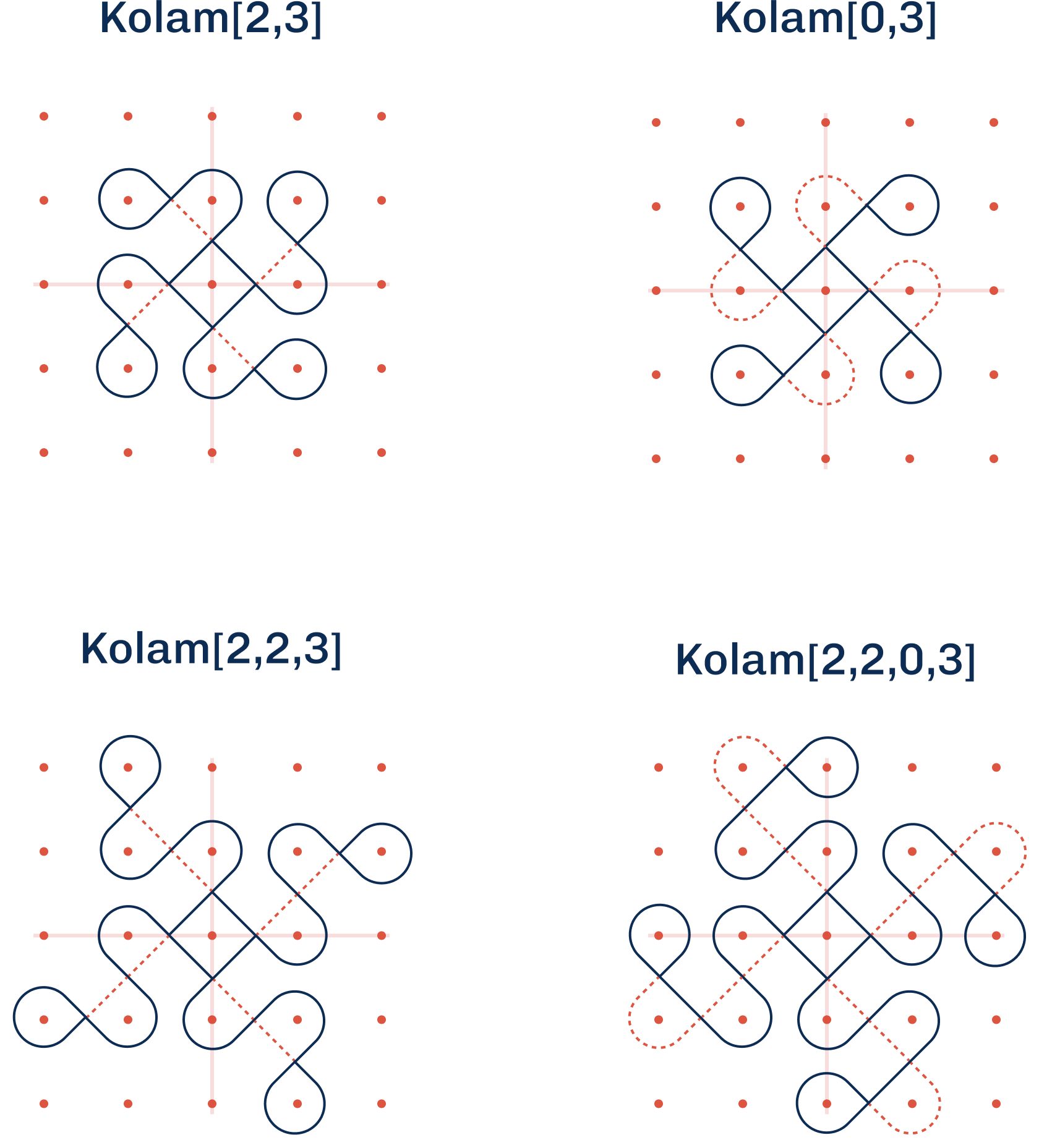
Figure 8 displays examples of Kolams constructed using forward path types. Notably, Kolam[2,3] and Kolam[0,3] appear as mirror images of each other, reflecting the complementary nature of the path types used to close the loop in each case.
This systematic approach has been implemented using Python’s Turtle graphics library, where the number of path types determines the Kolam’s size. The system processes user-inputted sequences as arrays, completing the Kolam by computing the path types needed to close the loop based on the specified path types. Each path type corresponds to a distinct element in the input array. The current model operates under the assumption that forward paths do not intersect with adjacent quadrants, or that any such intersections do not create conflicting geometry. When intersections do occur, the resulting Kolam remains geometrically valid but may split into two distinct loops rather than maintaining a single continuous path. This splitting phenomenon represents multi-loop Kolam structures, an advanced topic for future exploration.
Number of path types: 7 Sequence:
[2,1,0,2,1,0,2]
’’ Figure 9: Turtle graphics to draw Kolams with numerical inputs
Complex Kolams may require multiple continuous line drawings to achieve completion. This occurs when the primary path intersects with itself during construction or returns to its starting point, creating closed segments that leave certain pullis unencircled.
In these instances, additional loops must be drawn to encircle the remaining pullis, with existing closed paths serving as geometric constraints for subsequent loop construction. This approach incorporates diverse symmetrical relationships and continuity principles across multiple interconnected loops.
Figure 10 illustrates a Kolam comprising three continuous line drawings, demonstrating how loop intersections ensure complete encirclement of all pullis. The figure shows Path type 1 being enclosed by two Path type 0 segments originating from different loops within the same Kolam structure. These multi-loop patterns reveal the sophisticated mathematical relationships underlying traditional Kolam construction.
Note: The detailed analysis of multi-loop Kolam structures, while beyond the scope of this current work, represents a significant area for future research in computational geometry and traditional pattern analysis.
The arcs and lines illustrated in Kolams resemble celetic knots, macrame knots and interlace patterns. There are several geometric references that can be correlated. In the turtle graphics code we have 3 arc types as inputs that interlace to a Kolam, this could resemble Arabesque patterns.
In this experimentation, we will use some structuring inputs of islamic So following the 4 fold radial symmetry and path type arcs from the basis of the kolam code, structuring a similar language for islamic interlace patterns. Of course islamic geometry is a vast subject on its own, this can serve as a mere starting point.


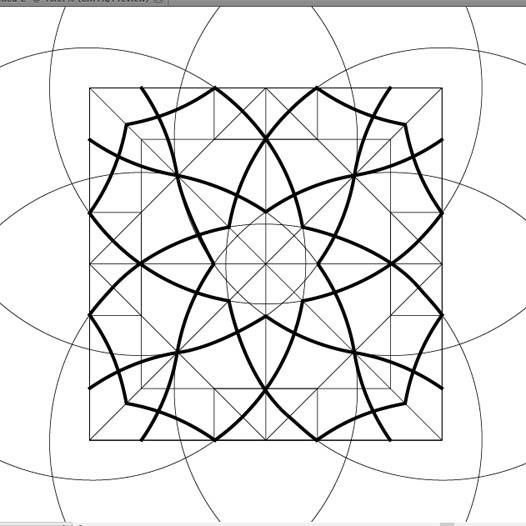
For this experiement, we will make use of the arc types and straight lines adjacent to the inputs for a Kolam. We will try to experiement with the similar recursion for getting the interlace and look at the output patterns.

The resulting patterns generated in turtle graphics were visually striking. While they preserve the core structural logic found in various forms of Islamic design—such as arabesques and girih—they are constructed through the procedural logic of Kolams, a tradition from a completely different cultural context. This cross-cultural approach demonstrates how shared systems of geometric reasoning can lead to the creation of novel pattern types, expanding both visual language and design methodology.
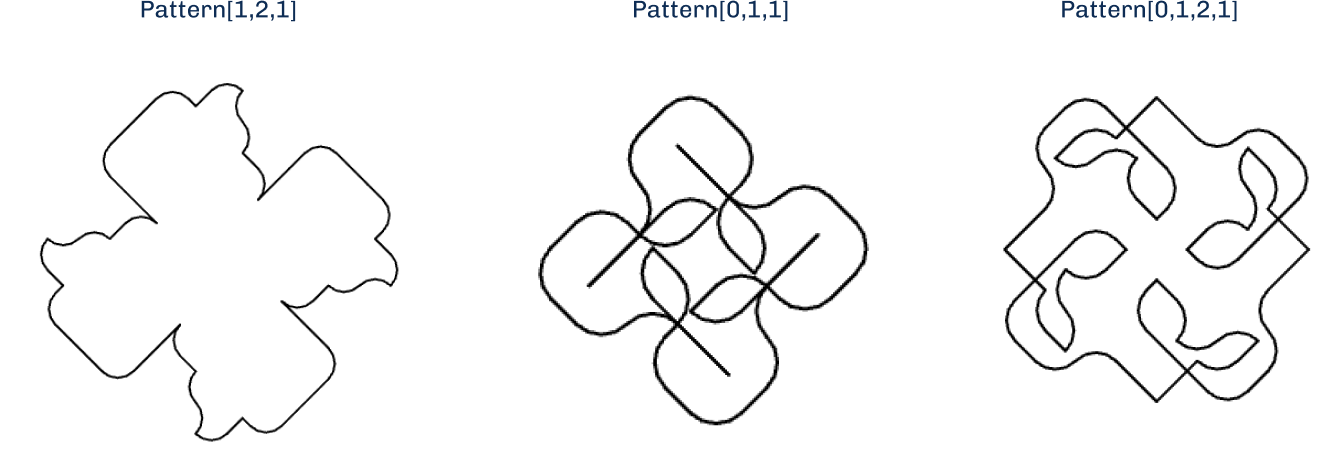
Number of path types: 5 Sequence:
[1,1,0,2,1]
’’ Figure 17: Turtle graphics to generate experimental patterns
The patterning system, derived from Kolam, already encodes path logic numerically, making it easy to map to motif systems like Islamic interlace.
The same radial symmetry, repetition, and motif sequencing used in Kolam can model Islamic pattern construction rules, such as:
The second modular construction method frames Kolams as tiling systems, where elements are tiles extracted from completed pattern forms. This reverse engineering approach, common in Kolam research, identifies 6 fundamental tile types shown in Figure 18. These tiles emerge from the mathematical permutations of rounded corners in a square: 4 corners allowing 4C2 combinations, resulting in 6 distinct configurations.

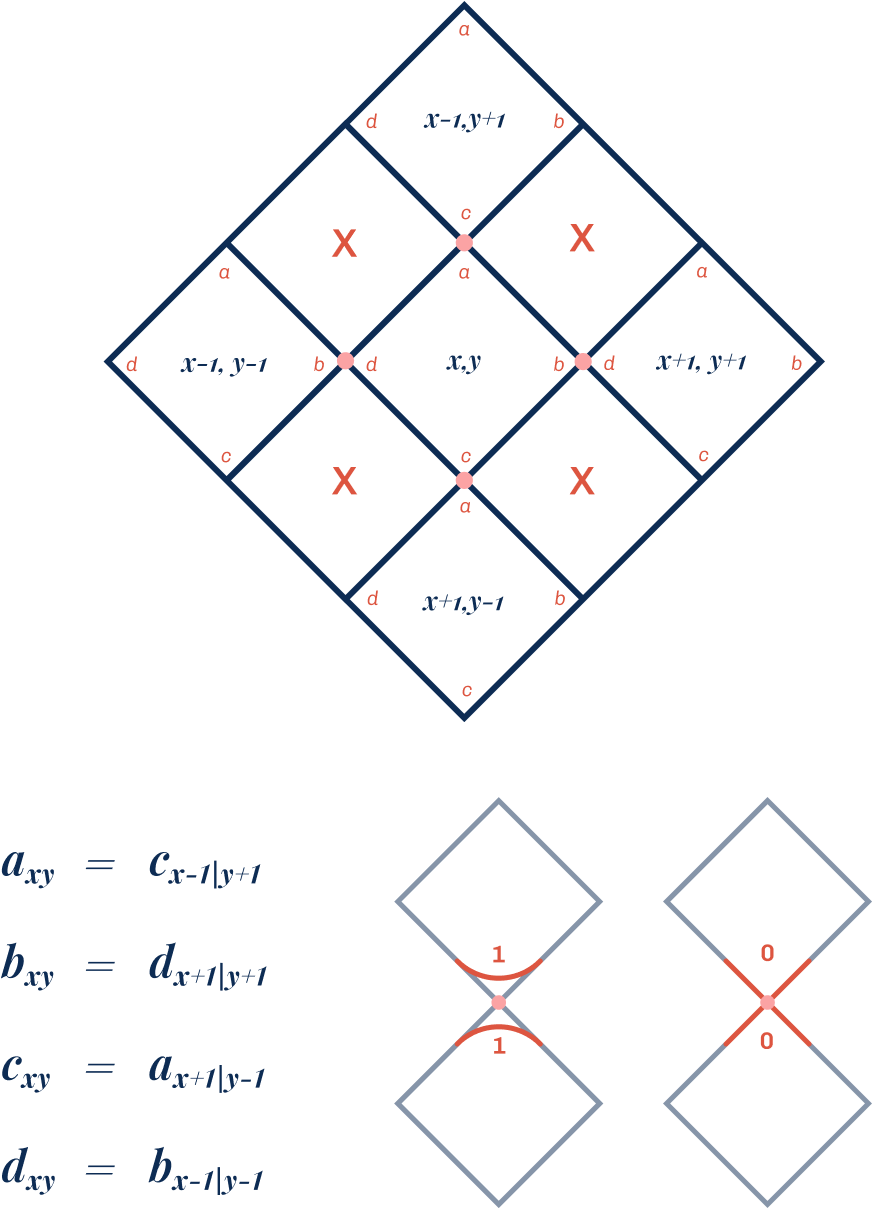
The tile shapes depend on the curved sides of a square, but for computational purposes in Kolam generation, orientation becomes crucial. Each square corner can be assigned a binary value: rounded corners receive the value 1, while sharp corners receive the value 0. With four corners labeled a, b, c, and d, each corner functions as a binary switch that can be either 0 or 1, creating the foundation for systematic tile generation.
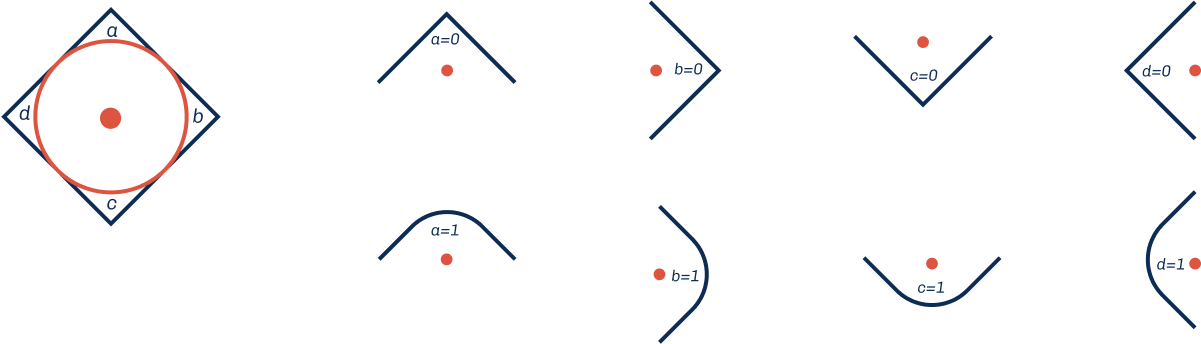
Each corner can exist in one of two states, and with four corners per square, this creates 2⁴ = 16 total permutations of tile shapes. This binary system mirrors hexadecimal notation, where each tile can be represented by a 4-bit binary number corresponding to its four corner states. Figure 10 displays all 16 possible tile configurations, each uniquely identifiable by its hexadecimal code equivalent (0x0 through 0xF), providing a systematic computational framework for Kolam tile generation.

The underlying grid framework defines the spatial constraints for Kolam tile placement. For Pulli Kolams, this foundation consists of a dotted grid where each tile centers on a dot point. Our computational framework positions tiles with their central dot serving as the reference anchor. Establishing the Kolam’s center at coordinates (0,0), the grid system functions like a Cartesian coordinate plane rotated 45 degrees. This diagonal grid orientation reflects traditional Kolam geometry while enabling precise computational control over tile positioning and pattern development.
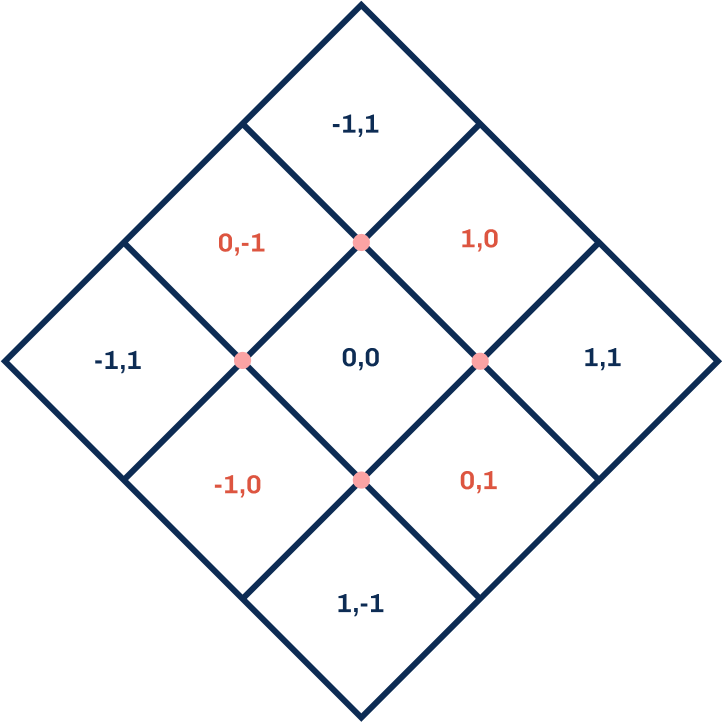
A critical constraint emerges from the pulli arrangement itself: the dotted grid structure prohibits tile placement at certain coordinates, maintaining the geometric integrity essential to traditional Kolam patterns. This spatial limitation reflects the mathematical logic embedded in centuries of Kolam practice.
With the grid positioning established, we must now consider both the tile’s location (x,y coordinates) and its corner configuration. We denote corner values using the notation axy, where ‘a’ represents a specific corner of the tile positioned at coordinates (x,y). To maintain Kolam continuity and authenticity, three fundamental rules govern tile placement:
The interface is implemented in p5.js. Edge values are adjusted by hovering and toggling between adjacent tiles. Pulli configurations may be selected and edges may be toggled iteratively until the desired Kolam pattern is formed.
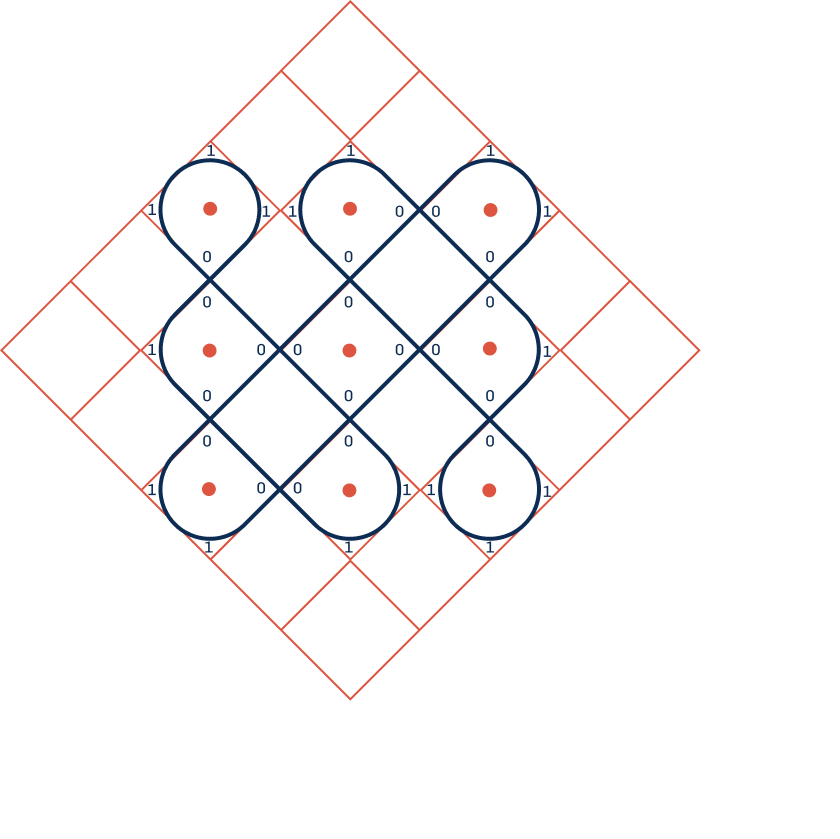
Figure 24: Interactive Kolam pattern generation tool created using p5.js.
When we approach Kolams through the lens of a tiling system, applying Truchet tiling becomes a natural and compelling experiment. Both systems use modular logic to generate intricate, rule-based patterns. However, Kolam construction typically involves sixteen distinct tile types, offering a broader range of variation compared to the two or four types found in most Truchet systems.
This is more than an experimental crossover. It reveals deep structural parallels and allows us to reframe Truchet tiling through a Kolam-informed process. By adapting Truchet inputs into the Kolam framework, we not only generate new hybrid forms but also make a case for a shared, cross-cultural design logic—a foundation for a more universal pattern language.

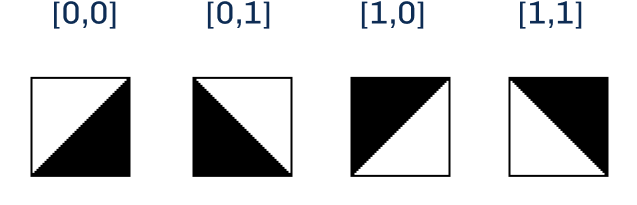
Figure 27: Interactive Truchet pattern generation tool created using p5.js.
Figure 28: Interactive Truchet pattern generation tool created using p5.js.
The result is a system in which inputs may be interchanged, yet the resulting visual language shifts significantly. This demonstrates how shared structural principles can give rise to outputs that are culturally distinct while remaining computationally compatible.
These experiments generate a wide range of visual forms, from the ritualistic to the abstract, and point toward a scalable design logic. This logic has the potential to accommodate additional tiling systems—whether cultural or algorithmic—within a unified, modular framework.
Kolam is a community-rooted practice embedded in daily rituals and passed down over generations, not the product of any single originator, but of collective knowledge shaped through time. Unlike individual-led frameworks of modern science, Kolam and other cultural pattern systems emerge from shared, lived experience.
Yet, much of contemporary research tends to interpret these systems through the lens of existing scientific frameworks by aligning them with Euclidean geometry, Cartesian coordinate system, or Hilbert’s curves. While such comparisons can offer useful translations, they often operate under an assumption that modern science is the default authority and that cultural practices are only valuable when they are used to validate it. This perspective is not only reductive; it limits the potential for discovery by framing knowledge as something to be fitted into pre-existing molds rather than expanded.
The goal here is to recognize these biases and to rethink research itself as a process that can honor, not overwrite, the systems it studies. Studying patterns like Kolams, Islamic geometric art, Navajo weavings, or African Kente cloth on their own terms allows us to see them as deep repositories of mathematical and aesthetic knowledge, crafted collectively, transmitted generationally, and evolving across time. Islamic geometry, for instance, is not only visually complex but also reflects centuries of mathematical understanding expressed through art and architecture. These systems are not static; they embody exchanges across cultures, trade routes, and time periods, each reinforcing the collaborative and cross-cultural nature of pattern-making.
Rather than trying to fit these practices into frameworks that prioritize individual authorship and formal institutional recognition, we should explore them as living systems of knowledge. Doing so opens up a world of possibility, not only to learn from these traditions, but also to imagine new ones that emerge from their intersection.
Consider how Truchet tiles, named after a European cleric, are easy to map into a Kolam-based framework. The reverse is far more complex: Kolams use 16 tile types and involve richer permutational logic. Yet, tools and AI still struggle to capture this complexity because it doesn’t fit neatly into pre-existing models. That doesn’t make Kolams less algorithmic—it simply means we need better ways to understand them.

By framing patterns as knowledge systems and using technology to support, rather than flatten, their richness, we can expand the boundaries of science, computation, and design. This isn’t just about cultural appreciation. It’s about transforming how we think about knowledge: as something that is communal, evolving, and shared. Discovery, after all, has always been a collective act.