Entangled Rituals: Visualizing Chance Through Quantum Algorithms

Abstract

This paper introduces some of my recent experiments with artistic visualizations of random chance probabilities, ritual heuristics and algorithmic thinking using quantum principles. Through history, digital culture and the mediated environment have long played the role of a kind of second nature in human society, shaping scientific thinking and technological progress, which also had its affects to mental models and the human experience. However, in recent decades we are starting to witness a shift in transcending classical dualism, binary systems, and the consensus on objective reality. The strange and unfamiliar concepts that can be found in quantum principles, are redefining our very concepts of objectivity, time and space, bringing new ways to frame problems, raise questions and propose solutions. After a period of rationalism and analytical reasoning, intuitive thinking as a direct mode of understanding the world, becomes increasingly important again, to compose resilient mental models and navigate complex, nonlinear scenarios. The latest achievements of quantum computation are reopening the core, ontological levels of experience - where regular logic is just a “frozen” state of a continuously changing, entangled reality. At the same time, this uncertainty can be found in many existing, forgotten disciplines, such as the ancient modeling methods of chance operations, combinatorics, generative grammars, astrology, the I-Ching, and many other procedural systems to navigate the metaphysics of the human condition. The following experiments¹ are playful attempts to interpret these concepts, from generating simple randomness to more complex algorithms that operate in computational space.

Randomness

To produce randomness³, most computer systems — including modern cryptographic protocols and generative art — make use of pseudo-random number generators (PRNGs). These are designed to generate sequences of numbers that appear random over large periods, but in reality they are driven by deterministic and predictable arithmetic. While regular computers are capable to generate pseudo-random values, there are methods to generate true randomness, like physical phenomenons such as dice, atmospheric noise or quantum principles (although hardware calibration problems can make the numbers predictable if they’re not fixed). The methods that are creating new numbers using quantum principles are usually called Quantum Random Number Generators or QRNGs. The first experiment in this paper is extremely simple, which can also be considered as an introductory “Hello World” program for quantum computing. Quantum randomness arises from the inherent uncertainty in quantum mechanics, particularly from phenomena like superposition⁴ and measurement collapse⁵. When a quantum system, such as a qubit in a superposition state, is measured, the outcome is fundamentally unpredictable, with probabilities dictated by the wave function. For example, if a qubit is prepared in an equal superposition state (|0⟩ + |1⟩), a measurement will yield 0 or 1 with equal probability, and there is no hidden variable determining the outcome beforehand. This experiment is generating a sequence of true random numbers by repeatedly measuring the superposition of a qubit, where the qubit collapses into a classical bit with a value of 0 (-) or 1 (+) upon each measurement. The left image shows the visualization of the resulting binary sequence from the experiment, while the right image shows the quantum circuit, made for the experiment in Qiskit⁶.

Divination Systems

To continue this approach, some context can be provided to the generated sequences. The next experiment introduces a conceptual layer to the process, where the goal is to create binary patterns in the forms of I Ching hexagrams. The I Ching employs a symbolic language, where abstract representations of complex, dynamic processes are described through chance-based generation of hexagrams. In the system of yarrow stalk divination⁷, the process involves repeatedly sorting and counting 49 stalks into groups, following a structured process to generate one of the 64 hexagrams, which are then interpreted for guidance on personal or cosmic matters. Graphically these hexagrams are usually composed of six lines, each of which can be either a solid line or a broken line. Each symbol acts as a metaphor for natural and human processes, capturing a vast range of interpretations within a single shape. Both the I Ching and quantum mechanics embrace true randomness and the observer’s role, suggesting that meaning and conventional reality takes form only through subjective interactions with an unfixed, probabilistic universe.

Apart of nondeterministic random generation using superposition, this experiment examines another key principle in the creation of binary sequences, by incorporating quantum entanglement. As a starting point, three qubits are put in superposition within a circuit, that will be capable to generate a sequence of three random binary numbers. On the other half of the circuit, each of the initial qubits has a connected qubit, entangled together, using a CNOT (controlled not) gate. Upon measurement, the first three qubits will collapse into a random binary sequence, causing their entangled counterparts to mirror the same pattern, forming a symmetrical hexagram. As mentioned before, qubits are highly sensitive to external factors like thermal vibrations and electromagnetic interference and maintaining perfect entanglement is still extremely difficult. Despite advancements in hardware and error-correction methods, quantum computers still encounter noise, leading to imperfections in the hexagram’s symmetry, these are represented visually with blue and black symbols. The process is accompanied by sonification, using sound synthesis (oscillators, filters, and amplifiers) to interpret quantum noise.

Quantum Walk

Even though the conceptual beauty to create true, nondeterministic randomness is compelling, from an aesthetic perspective, there is not so much we can leverage from this method that is differing from traditional, pseudo random generators. Typically, a classical random walk algorithm involves a person flipping a coin to decide whether to move left or right, and over many steps, their position follows a predictable bell-curve distribution. This could really be done with a physical dice or a pseudo random number generator, we could not really tell the difference from a quantum based approach. Things can become much more interesting when using as many qubits as the number of the steps we have in our random generating sequence. In a quantum walk⁸, the walker doesn’t just step left or right. Instead, they exist in a superposition of both directions at the same time, due to the quantum principles of superposition and interference. As opposed to perform each walking sequence individually, just like we could do with a classical computational approach, we can measure each step at once, and get a probability distribution over the whole computational space at the same time. This results in a fundamentally different exploration of possibilities, that can be used extremely effectively for searching, pathfinding or decoding passwords and classical cryptographical algorithms.

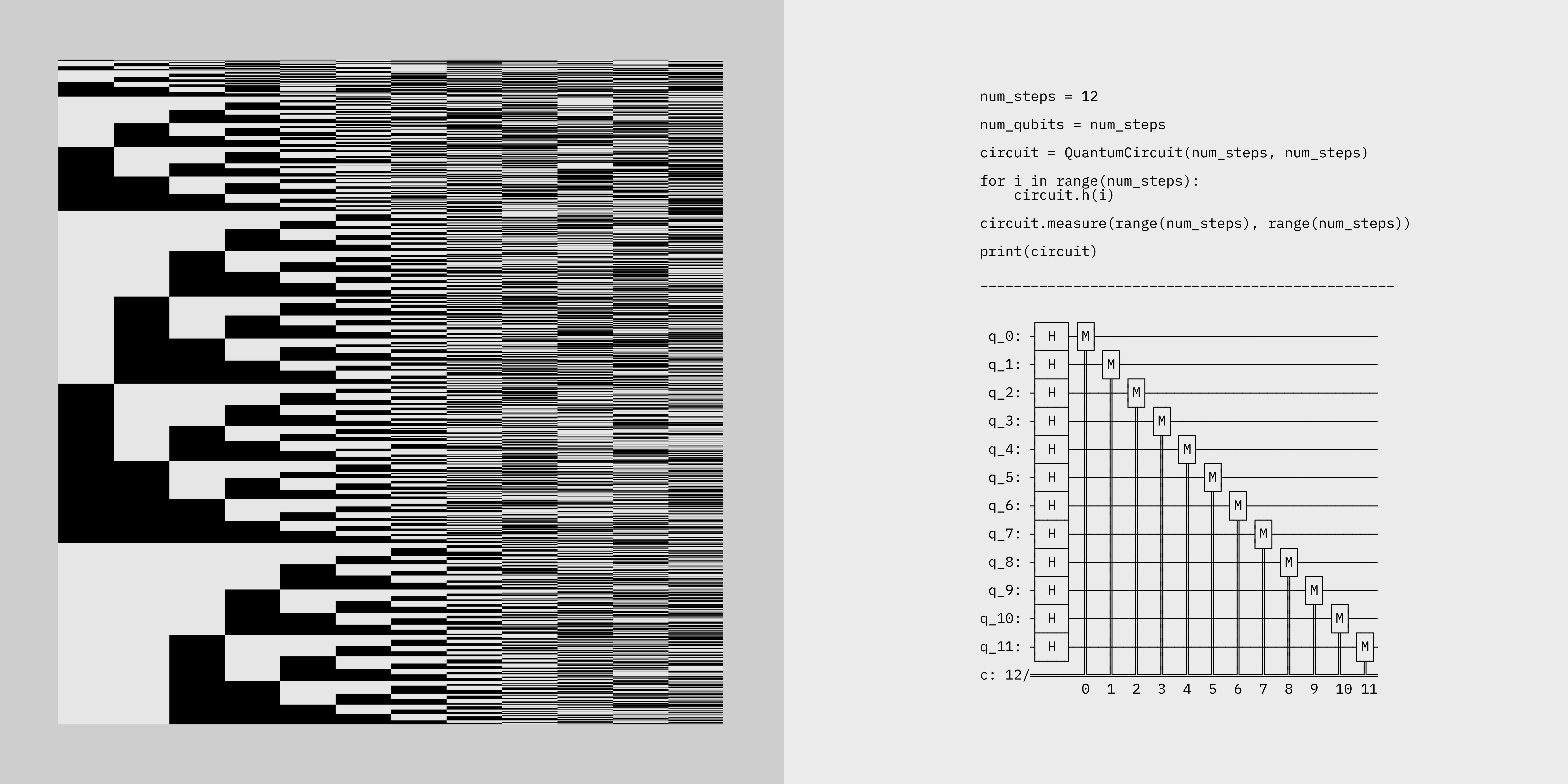
The visualization illustrates multiple possible outcomes of a twelve-step quantum walk sequence simultaneously, as they are collapsed upon measurement on a quantum processor. Afterward, the measurement results are rearranged for clearer representation: the most probable sequence appears at the top, while the least probable sequence is shown at the bottom. The steps in the sequences are performed from left to right, with black shapes representing 1 and white shapes representing 0 in each pixel line.

Conditional Space

A one-dimensional cellular automaton⁹ (1D CA) is a simple yet profound model used to explore conditional space and the nature of computation. It consists of a line of discrete cells, each holding a binary state (typically 0 or 1), which evolve over time based on a fixed rule that considers the states of neighboring cells. Despite its simplicity, a 1D CA can generate an astonishing range of behaviors, from repetitive and predictable patterns to chaotic and highly complex structures. This makes it a powerful tool for investigating how complexity emerges from simplicity, and how conditional logic—encoded in local update rules—can give rise to global phenomena. Crucially, some 1D CAs are computationally universal — capable of simulating any Turing machine — highlighting their relevance not just in modeling, but also in theoretical computer science. Stephen Wolfram’s classification of cellular automata emphasizes this point, showing how certain simple rules (like Rule 110) can encapsulate the core of computation itself. By abstracting computation to spatially extended, time-evolving patterns, 1D cellular automata invite us to rethink computation as a distributed, condition-driven process, rather than a centralized, instruction-based one.

In a classical CA, each cell follows a strict, deterministic rule that maps a local configuration (typically the states of a cell and its immediate neighbors) to a single binary outcome. Over time, these rules unfold across the array of cells, producing structured patterns that can be repetitive, chaotic, or even computationally universal. When such classical automata are implemented on quantum hardware — by encoding each classical bit as a qubit and simulating logic gates like the CCCNOT (Toffoli-3 or 3-controlled NOT gate) — they retain this determinism. The evolution is reversible and logical, but not genuinely quantum; the quantum hardware merely mimics classical behavior, and does so inefficiently, as the full potential of quantum superposition and entanglement is unused. Still, this approach demonstrates how classical logic can be embedded within the quantum substrate, serving as a bridge between computational models.

In contrast, a quantum elementary automaton departs from determinism by initializing qubits in superposition. Rather than evolving along a single deterministic path, the system simultaneously explores a spectrum of possible configurations, each with a corresponding probability amplitude. The same local rules are applied, but now they act on qubits in uncertain states, producing interference and entanglement. The outcome is no longer a single path through rule space, but a probabilistic landscape. Measurement collapses this rich structure into a definite binary output, but until that point, each cell represents a blur of possibilities. Visually, this is represented through brightness or opacity: a cell glows in proportion to the probability that it will be observed in state 1. This indeterminacy is emphasized through sound synthesis within the experiment, using oscillators, filters and modulators in response to probabilistic dynamics, evoking a more fluid and expressive understanding of computation as something more than logic, more like a wave of potentiality.

The contrast between these two modes—deterministic versus probabilistic—is not merely technical but philosophical. The classical CA is an engine of certainty, where each step follows inevitably from the last. The quantum automaton, by contrast, reflects a universe where possibilities coexist and outcomes are weighted rather than fixed. Where the classical model explores conditional space as a branching tree of logical consequences, the quantum model immerses itself in a probability cloud, where the path only crystallizes when observed. This makes the quantum automaton a deeply evocative model for understanding how rules can operate within ambiguity, and how computation itself may be reimagined as a process of collapsing potential into form.

Nondualism

The contrast between classical and quantum approaches reflects two distinct paradigms of computation itself. Classical computation is rooted in determinism and discrete logic—systems evolve through a sequence of well-defined, causal steps, each outcome fully determined by prior conditions. It models the world as something that can be fully analyzed, predicted, and constructed from simple rules. Quantum computation, on the other hand, reframes the process as fundamentally probabilistic and relational. It leverages superposition, interference, and entanglement to operate within a space of possibilities rather than certainties. This suggests that computation need not be confined to stepwise logic, but can also emerge from patterns of potentials and interactions.

Beyond practical, mathematical affordances of quantum computing, their underlying structure can resemble general, ontological concepts that can be found in the philosophical schools of non-dualism. Found in traditions like Advaita Vedanta, Zen Buddhism, and Taoism, non-dualism holds that reality is not composed of independent, separate entities but is an indivisible whole. This aligns with quantum mechanics, where particles do not have definite states until observed, and quantum entanglement suggests that separated particles remain fundamentally connected beyond classical space-time constraints. Just like quantum algorithms, operating the system of I-Ching does not provide fixed answers but rather patterns of transformation, emphasizing that all distinctions dissolve into an interconnected reality — it’s not only a way of manipulating symbols, but also a way of understanding the present, where there are different levels of reality and our perception of it can change depending on the perspective we take.