Thinking About Fractals (Fabric is Fractal)

Patricia Bentley

Cloth moves. It ripples in space, now flat, now bunched, draping around and taking the contours of its host. Like a soft cloud it resists exact measurement, seeming to expand and contract as it swirls. Like the surface of a balloon it stretches out then shrinks back without breaking.

Cloth behaves like a fractal: its pliability comes from the self-similarity of its iterations. It is made of a tiny crossover of one thread over another, repeated many times in an algorithmic pattern that makes a structure. Each set of four crossovers, over then under, is a right-angled square that replicates the larger piece of cloth that it is a part of (Figure 1).

A piece of cloth is paradoxical, being of both two and three dimensions – or inhabiting a fractional space between them. When flat, it is two-dimensional, having only an area. As soon as it is moved, even slightly, it acquires volume.

Cloth is fractal, but it is not mathematically fractal like a computer simulation or a drawing on a page. It is a real-world, therefore approximate, fractal object.¹

In this study, I am imagining cloth as a fractal. That is to say, if cloth were a fractal, it would behave in this way. Certainly there is something enigmatic about this stuff, taken for granted as it is – yet wrapping every single one of us, humans, in its folds, in one way or another, for our entire lives. Two points are important for me to make here: my study has no interest in fractal-influenced designs applied to or printed on cloth. Rather, I posit that cloth is fractal by virtue of its construction, as evidenced by Figure 1. Secondly, I am primarily concerned with cloth as clothing material, wrapping around the body: its iteration, its fractal dimension, its topology, and its touch. I will show how all of these qualities are related to each other.

What is a fractal?

A fractal is an idealized mathematical object that exhibits properties of fractal geometry. These properties differ markedly from those of classical geometry. The main fractal characteristics include fractional dimension, deformability, self-similarity, and iteration. Claude Heiland-Allen gives a comprehensive introduction to an influential mathematical fractal, the Mandlebrot set.²

The starting point for textile construction is iteration – a series of instructions to repeat an action – thereby building a piece of cloth by performing what Deanna Gelosi calls its inherently algorithmic nature.³

Fractal (fractional) dimension in cloth

An object’s measurability (its length, area or volume) and its dimensionality (one, two, or three dimensions) are fixed in the everyday world, but in the fractal domain, these properties do not hold. An object with fractal dimension has measurements that are dependent on the scale of measuring. The most frequently used example of this phenomenon in the natural world is the length of a coastline: the more you zoom into every little bend and bump, the longer is the measurement that results. Calculating the exact fractional dimension uses logarithmic scales; a detailed discussion of that operation is beyond the scope of this study, but an excellent description is in Falconer.⁴

The Sierpinski triangle, a paradigmatic mathematical fractal, illustrates how fractal dimension develops from iteration: it proceeds according to the instructions of the formula:

The results are put into the function and run again. As the shapes are fed back into the triangle, it gains perimeter from the smaller triangles, but it decreases in area, becoming increasingly “holey.” (Figure 2). If a random number is introduced into a fractal construction, it progressively assumes a more natural appearance.⁵ The triangle on the right shows this effect.

The triangle on the right looks crumpled. In a paradoxical twist that exemplifies the nature of fractal geometry, it appears to have gained volume to occupy 3-D space even though it has lost area because of all those triangular removals. Ibrohimova and Asatov discuss this paradox in reference to cloth.

If we continue to run the function for Figure 2, the mathematical triangle will continue to get increasingly “holey” but never completely fall apart. In the case of an actual textile, the more and more crumpled cloth will finally fall apart into dust. This disconnection is another fractal quality. The first mathematical fractal, conceptualized by Georg Cantor, demonstrates the way this happens, by removing the middle third of a line until only a dust of points remains (Figure 3).⁷

Fractal creation has a playful, game-like quality to it. Weaving too is a game of patterns,⁸ but it proceeds in a completely different way from a Sierpinski triangle or a Cantor set – or, the modularity is of a different nature, being one long thin thread at a time laid at right angles across another set of threads (Figure 4). But it always has holes or spaces in it. This “holey-ness” or porosity is a feature of its topology, which I will discuss in a later section.

Fractal self-similarity

The Sierpinski triangle and the Cantor set race surprisingly quickly towards infinitesimal dimensions in their iterations and will continue to infinity. By the same token, a right-angled section of loom-woven cloth is self-similar in structure to the cloth at every diminishing scale, down to the individual thread interlacement (Figure 1). Fractal self-similarity is one of the ways that fractal geometry describes the patterned yet irregular aspects of nature.⁹

However, any natural object will only display self-similarity within a particular range of scales. An approximate fractal object like cloth will “bottom out” at very fine scales, losing its self-similarity to appear as what it is: molecules and atoms.¹⁰

Topology

Woven cloth’s topological nature is a defining characteristic, more than its shape or its size. A topological object preserves its properties when it is deformed in some way. For example, the porosity of a textile, the number and size of spaces in between its threads, does not change if it is deformed by stretching or crumpling, even if the shape of those spaces is altered. This is important for the analysis of natural materials like soils, in order to assess fluid movements though the pores.¹¹ In the case of cloth, air is what flows through the pores, and this action impacts its touch and texture.

Not all textile materials are pliable to the same extent; reed for baskets is relatively rigid while threads and yarns are relatively limp. This affects a cloth’s deformability, and links it to a branch of topology that studies purely mathematical knots (a conceptual knot has no ends). Cloth can be thought of mathematically as “a specific case of knots or links.”¹² A good introduction to knot theory is online at ‘Why knot: knots, molecules and stick numbers.’¹³

In knot theory, an ’unknot” is a simple closed circle of string with no joins. A trefoil knot has two crosses and cannot be untied to become an “unknot.” Of course a trefoil knot does not exist in the real world – but loom-woven cloth mirrors this special quality: once the warps and wefts of a piece of cloth are woven together, you cannot change their position without breaking them. The cloth is deformable, but its connectivity must not be broken.¹⁴

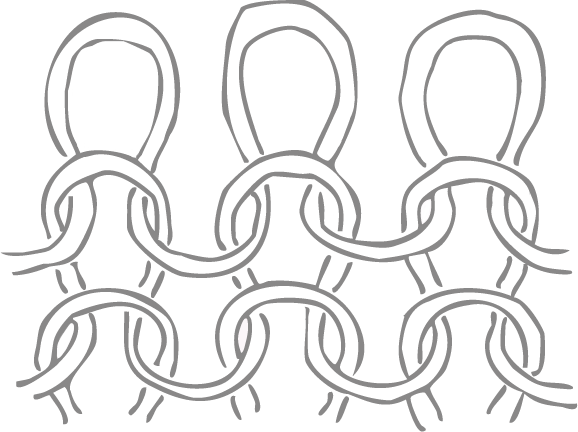
As well as connectivity – which defines how spaces are linked – and deformability – which defines how they distort – “loopiness” is a topological feature of fractals.¹⁵ Loopiness is an apt word to use when describing cloth’s fractal nature– knitted cloth is literally made of loops (Figure 5). The term also refers to feedback loops, or recursion, the essential method of iterating shapes to create a fractal object.

Ron Eglash notes that Ghanian kente cloth looks like the design was drawn on a rubber sheet which was “half stretched and half contracted.”¹⁶ This, again, is the topological feature of deformability. It also illustrates the fractal feature of self-similarity. Here Eglash is referring to the cloth’s pattern, but it is a pattern that is made by the woven structure rather than by paint or print (Figure 6).

Touch

Cloth touches the body. Its relative roughness or slipperiness results from the number of points of contact it makes with the skin, and this is a factor of its fractional dimension as well as its topology and porosity.¹⁷ The experience of touch unites all of cloth’s fractal characteristics: its fractional dimension enables it to be both flat, so as to carry patterns on its surface, and shaped, to better deliver comfort and warmth to the body. Its self-similarity, a modularity that introduces many tiny spaces, gives it pliability.

In a sense, touching cloth and feeling it – with the whole body – enables a deep knowledge of it that the dominant sense of sight cannot reach. One realizes that it is made of patterns conforming to the rules of Euclidean geometry, but that it slips out of that harness as soon as it moves, and it veers toward fractal geometry with its uncertain relationship between area and volume. This is “embodied knowledge,” a field of cognitive research that investigates the primacy of touch in the human experience ¹⁸.

Art and Science

The fractal nature of fabric finds connection to other research areas as well, especially the closely related fields of visual art, cognitive science, and embodied cognition. Barbara Maria Stafford could be talking about fractal behaviour when she notes, “Art has had a longstanding role as an almost magical coordinator as well as concentrator of elusive, shifting, and out-of-phase experiences” ¹⁹.

In the historic and contemporary “Western” hierarchies of fine arts and crafts, textile arts have always held an ambiguous, even lesser position, but when they are viewed through the lens of fractal geometry, their very out-of-phase-ness becomes a strength. They begin to look like very intriguing objects indeed.