3D Patterning in the Cosmoscope

Introduction

Physical Design

The Holohedron (the physical artifact of the Cosmoscope project) is a spherical metal sculpture approximately 3.5 metres in diameter, weighing two tons and containing 2000 RGB LEDs mounted within a complex structure of intersecting metal rings of various sizes and orientations. In effect, it is a three-dimensional display whose LEDs are laid out geometrically, but not according to any kind of cartesian grid, and not spaced regularly in any dimension. Instead, the LED positions are specified through a series of mathematical equations, placing them around circles which are oriented at various geometric angles.

Based on the equations for the geometric form, every LED’s position can be determined in three dimensions. The circles themselves are actually positioned on the faces of nested tetrahedra within the device’s enclosing sphere, so there are internal triangular surfaces which could be addressed as flat irregular low-resolution display “screens” - and we do this, as described later.

The resolution and spacing of the LEDs makes it unsuitable as a display for realistic visual assets (still images or video), and in any case the project’s research topic (natural phenomena on scales that are either pan-galactic or microscopic) does not lend itself to photorealistic imagery.

The LEDs were driven by Novastar A45 receiving cards in four video wall driver systems and a MCTRL300 LED Display Controller³. We had to generate pixel-perfect bitmaps to an HDMI output to drive the visual display. A major complication in programming the Holohedron was the physical wiring of the LEDs. Approximately fifty LED strips were threaded through the structure, following a pattern laid out by the AV company in charge of the lighting installation, and not directly related to the mathematical enumeration of the LEDs. As a result, a mapping had to be drawn up between the two-dimensional addressing of the LEDs in the driver hardware (strip number and offset) and the three-dimensional position of each LED. The mapping was constructed manually by observation, LED by LED.

Pre-Visualisation

The display system was developed using a pre-visualisation “digital twin” of the hardware, written in ClojureScript and rendered using THREE.js in a web browser. We dispensed with any development effort that would be required to render realistic shadows or propagation of illumination: that would be a complex undertaking, and given the abstract mathematical nature of the display material, we were confident that something which looked good on screen would also be compelling on the physical structure. This indeed turned out to be the case.

Visual Concept

Given the Holohedron’s weakness for displaying any realistic visual assets, we opted instead for abstract material of an algorithmic (equation-based) or geometric nature. We contemplated the pre-rendering of material, but we were faced with building our own software to do so, so it made sense to just do the visual generation directly on-device in real time. This made synchronisation to the dynamically-generated soundtrack easier, but a downside was a lower-than-ideal final frame rate (approximately 10 frames per second on 2017 hardware) due to the CPU load of calculating LED values - there was no obvious way to bring a GPU to bear on the task. In fact, some of the more CPU-intensive generator functions were implemented in Emscripten⁴, called via a ClojureScript wrapper.

We developed two distinct rendering models: one which targeted a virtual 2-dimensional surface, and one which rendered into the device’s enclosing three-dimensional sphere. These models were not mutually exclusive: the 2D render was a specific mapping within the 3D scheme, so animations of both kinds could be shown simultaneously, and multiple 2D animations could run at once. (One higher-order mapping we developed supported square visuals which were then “folded” along a tetrahedral edge and onto two triangular sides.)

This kind of mapping scheme was informed by the way we built Plenum (although it’s a fairly obvious approach and has no doubt been used in digital art elsewhere: the interested reader is referred to the literature on scalar fields). Here, any displayed pattern on a canvas of discrete points is implemented as a function from a point’s position to the displayed value. In the image of Plenum below, the display function maps point position (x,y) to point size, so even though the points are arranged irregularly, and are constantly moving, visual artifacts like the concentric rings remain in a stable position.

Such scalar field functions have numerous advantages:

• they are compact (compared to almost any representation of the data points)
• they are impervious to changes in the display geometry (and are therefore “portable” between installations)
• they can be mapped and composed in numerous ways to generate new functions (and we can build higher-order combinators over them)
• we can produce time-based animations by adding a further parameter t representing time

The Holohedron operates via combinators over scalar functions in (x,y,z,t), where t is time, and we have a variety of test animations, such as those using trigonometry to rotate visual elements, or produce periodic animation patterns (with trigonometry over t). That gets us from a “model” parameter space operating in three-dimensional Cartesian space (and possibly implemented in Emscripten, as we described earlier) to the internal surfaces in the Holohedron.

As an example, suppose we really do want to draw things accurately on one of the triangular faces. We can do that by doing our drawing in Cartesian space, in one plane (with, say, z=0 for simplicity) and then shifting the appropriate part of the plane into the coordinate system of the Holohedron itself using an affine transformation. Here is an illustrated example: we have a generator function which lights up the X-Y plane, by returning 1 for all points very close to z=0 and 0 otherwise. (For now we’re working in monochrome, for simplicity; the generators can switch between scalar and RGB colour values as needed.) To illustrate that, we temporarily replace the Holohedron form with a 3D Cartesian point grid (since our entire rendering system is agnostic of the final layout of light sources):

Now we need to shift this generator function from the z=0 plane to a plane which coincides with a face of the Holohedron. Here’s what that looks like if we keep the Cartesian grid in place:

And now let’s swap the Cartesian grid out and put the Holohedron (or rather, cut-down a tetrahedral rendering of it) back:

And here’s the code:

(def tetra-plane
  (gx/affine-generator [[-1 -1 1] [1 -1 -1] [-1 1 -1]]
                       [[-1 -1 0] [1 1 0] [1 -1 0]]
                       (gx/z-proximal-generator 0
                         (gx/wrap-basis-fn 0 (fn [x y z t] 1.0)))))

Let’s read that from the inside out. (fn [x y z t] 1.0) is the initial generator which just outputs white (1.0) everywhere. The z-proximal-generator transforms that into a generator which puts out its value of 1.0 near the z=0 plane and fades it to zero away from that plane. Then the affine-generator shifts the display. Anything we look at on the plane [-1 -1 1] [1 -1 -1] [-1 1 -1] (the Holohedron tetrahedral plane) will be calculated by looking at the enclosed generator on the plane [-1 -1 0] [1 1 0] [1 -1 0], which is specified by a triangle of three distinct points where z=0.

The affine mapping is beyond the scope of this paper, but we should explain the wrap-basis-fn call. The functions over (x,y,z,t) which we’ve called “generators” are better described as “basis functions”. (That’s not an accurate use of the mathematical term, but we stole the usage from Jitter⁵.) Once we started working in Emscripten, it became clear that we’d probably be working with generators which have a non-trivial iteration from one time interval to the next (and possibly side-effecting too). An obvious example of this is Game of Life, which of course we were compelled to implement. So, it made sense to separate the advance of time from the “sampling” operation at (x,y,z). Hence, generators. (Think of this as currying a function over t as first argument.) This is the Clojure protocol:

(defprotocol GENERATOR
  "Generator form which separates time progression from x/y/z sampling."

  (locate [this t]
    "Locate to time `t`, return new state. (For Emscripten generators,
     may well just side-effect.)")
  (sample [this x y z]
    "Sample state at current time and `(x, y, z)`. Return single value
     or RGB triple."))

It’s trivial to take a basis function over (x,y,z,t) and turn it into a generator:

(defn wrap-basis-fn
  "Wrap a simple `(x, y, z, t)` basis function into a `GENERATOR` form."
  [t f]
  (reify GENERATOR
    (locate [this t']
      (wrap-basis-fn t' f))

    (sample [this x y z]
      (f x y z t))))

And so to the money shots. We have a Game of Life implementation, which plays Life in the X-Y plane while scrolling successive generations through Z. Rendered into our Cartesian grid, it looks like this:

Figure 5: Game of Life with History

(The reason that some of the points are grey is that for some reason we set up Game of Life to run with a grid size of 9 but the pixel grid has size 11, so the renderer is interpolating.)

How do we get this mapped onto one of the internal tetrahedrons of the Holohedron?

1. extract one slice (generation) of the game, using the Z proximal generation mentioned above
2. cut this slice along a diagonal, resulting in two right-angled triangles
3. affine-map each triangle to a face of the tetrahedron, making sure that the original hypotenuse edges are reattached on a single tetrahedron edge

This is the result:

Figure 6: Game of Life Wrapped to Tetrahedron

Scene Changes

The Holohedron installation operated for several hours at a time during a schedule where it was powered on and visible to the public. Running a single animation would be boring after even a short period of time, we had developed several different animations that we wished to display, and the brief for the project required some overall sequenced journey through different visual displays.

Over the last few weeks building up to the premiere of the project, we built a large number of animation patterns for the Holohedron structure, all in the form of generator functions. We needed a way to do some kind of automation-based mix between them, mediated by external control messages coming in as musical cues from the audio system.

We were also concerned about performance - the frame rate is not that high - and so only wanted to run generator functions whose effect would be visible at any one time, and effectively “mute” the others.

In the end, we opted for a 2D mixing scheme inspired by Audiomulch’s Metasurface⁶, which allows preset parameter values to be laid out as points in 2D space, so that a cursor position in the space determines a “mix” between presets according to distance from the cursor:

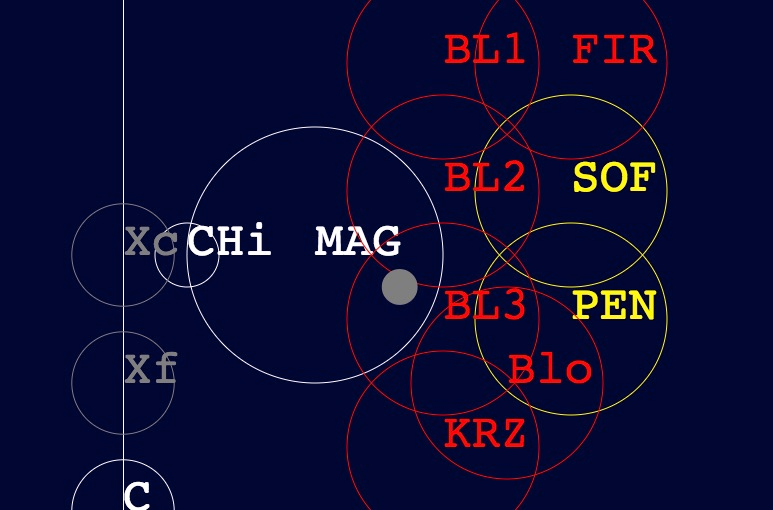
We manually laid out our animations on a 2D “terrain”, giving each of them an X/Y position and a radius. In some cases the animations overlapped and would play - or crossfade - at the same time.

Our generator functions already took parameters for spacial position (for each display point), and elapsed time. We added another two: distance and compass heading of the animation relative to the terrain cursor. An animation could choose to treat this navigational distance as an instruction to fade in or out (and in fact, we had a higher-order generator which applied a fade according to distance). And any animation out of range of the cursor was ignored for the purposes of rendering.

Cues from the audio system came in to the host machine via OSC; we used a Max patcher to turn that into a web socket message in order to get it into the browser. Every cue would kick off a cursor move to a specific X/Y point to take place in a time T. (Our almost-throwaway project Twizzle⁷ was a perfect tool to support the cue following.)

The actual hardware control was via video capture, using the NovaStar controller to send data signals via ethernet to the LED controllers. We ran the pre-visualisation full-screen in the Chrome browser, mirroring output to the HDMI capture device to drive the installation.

To generate the pixel patterns for the controller we put another HTML canvas into the application page, brought up a 2D drawing context, and drew into it by fast-updating an RGB byte array:

We conclude with a time-lapse video of the Holohedron in action.

Figure 10: The Cosmoscope Holohedron in Action